Discrete Conformal Equivalence of Polyhedral Surfaces

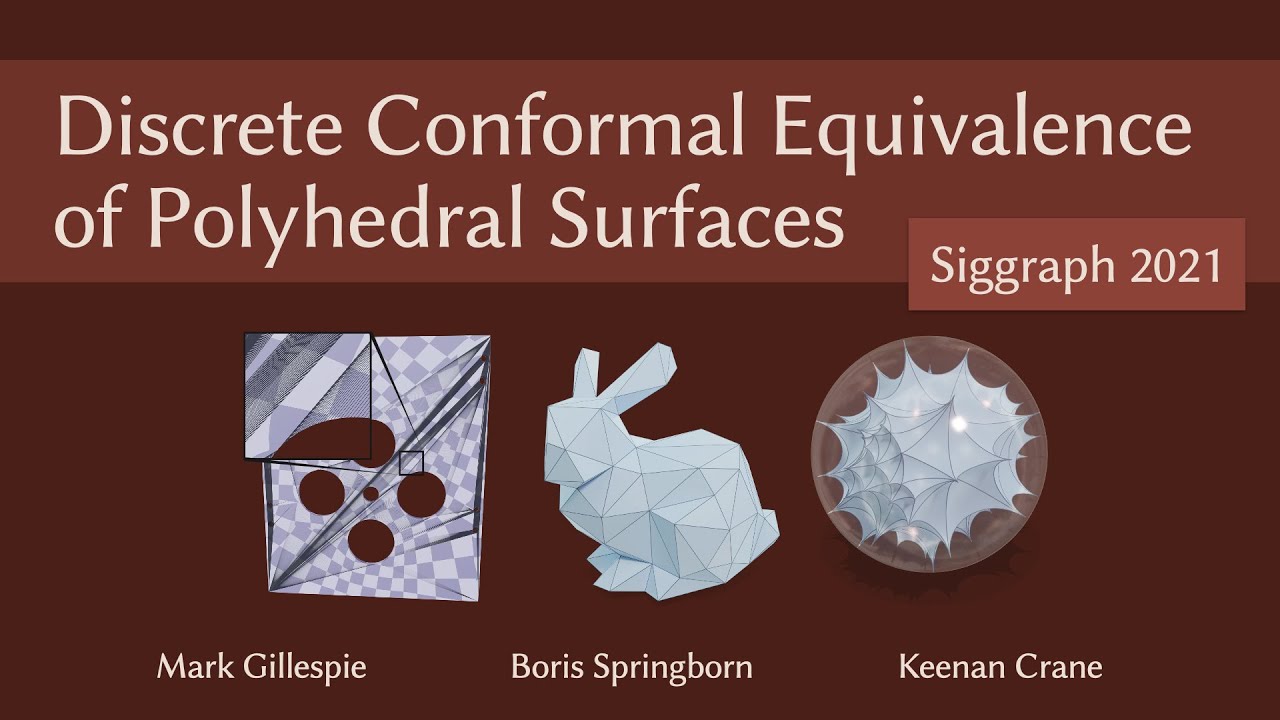
Discrete Conformal Equivalence of Polyhedral Surfaces by Mark Gillespie, Boris Springborn, and Keenan Crane. SIGGRAPH 2021.

This paper describes a numerical method for surface parameterization, yielding maps that are locally injective and discretely conformal in an exact sense. Unlike previous methods for discrete conformal parameterization, the method is guaranteed to work for any manifold triangle mesh, with no restrictions on triangulation quality or cone singularities. In particular we consider maps from surfaces of any genus (with or without boundary) to the plane, or globally bijective maps from genus zero surfaces to the sphere. Recent theoretical developments show that each task can be formulated as a convex problem where the triangulation is allowed to change—we complete the picture by introducing the machinery needed to actually construct a discrete conformal map. In particular, we introduce a new scheme for track- ing correspondence between triangulations based on normal coordinates, and a new interpolation procedure based on layout in the light cone. Stress tests involving difficult cone configurations and near-degenerate triangulations indicate that the method is extremely robust in practice, and provides high-quality interpolation even on meshes with poor elements.

[DPrintcomvideos]

This is fantastic. Really wonderful explanation.