filmov
tv
Integral of sin^4(x) using the power reducing identities to integrate an even power of sine.

Показать описание
Given an integral of an even power of sine or cosine, we know we're stuck using the power reducing identities sin^2(x)=1/2*(1-cos(2x)) and cos^2(x)=1/2*(1+cos(2x)).
In this problem, we compute the indefinite integral of sin^4(x) by using both power reducing identities.
In the first step, we split sin^4(x) into sin^2(x)*sin^2(x), then we apply the identity sin^2(x)=1/2*(1-cos(2x)) to each term. This yields an integrand with two terms whose antiderivatives are easy to guess, plus a remaining term with a cos^2(2x).
The squared cosine term requires us to apply the identity cos^2(x)=1/2*(1+cos(2x)), but this time the angle is 2x, so twice the angle is 4x! We apply our second power reducing identity, and now all terms in the integrand are quickly guessed using the chain rule backwards.
We clean up the final answer, and we're done computing the integral of sin^4(x) (aka the integral of (sin(x))^4).
In this problem, we compute the indefinite integral of sin^4(x) by using both power reducing identities.
In the first step, we split sin^4(x) into sin^2(x)*sin^2(x), then we apply the identity sin^2(x)=1/2*(1-cos(2x)) to each term. This yields an integrand with two terms whose antiderivatives are easy to guess, plus a remaining term with a cos^2(2x).
The squared cosine term requires us to apply the identity cos^2(x)=1/2*(1+cos(2x)), but this time the angle is 2x, so twice the angle is 4x! We apply our second power reducing identity, and now all terms in the integrand are quickly guessed using the chain rule backwards.
We clean up the final answer, and we're done computing the integral of sin^4(x) (aka the integral of (sin(x))^4).
 0:06:24
0:06:24
 0:07:39
0:07:39
 0:04:19
0:04:19
 0:03:36
0:03:36
 0:00:11
0:00:11
 0:04:07
0:04:07
 0:03:31
0:03:31
 0:02:55
0:02:55
 0:04:33
0:04:33
 0:03:48
0:03:48
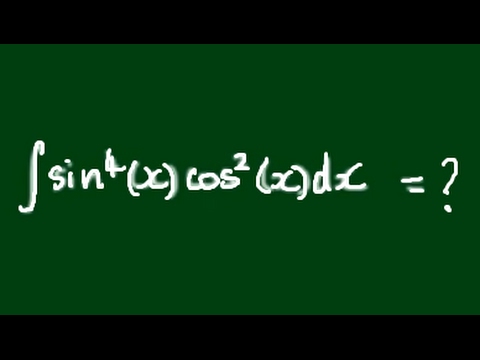 0:10:11
0:10:11
 0:03:55
0:03:55
 0:05:38
0:05:38
 0:06:53
0:06:53
 0:05:30
0:05:30
 0:31:29
0:31:29
 0:01:50
0:01:50
 0:02:16
0:02:16
 0:04:34
0:04:34
![int[sin^4(x)]](https://i.ytimg.com/vi/Lwmn-ZTCBMI/hqdefault.jpg) 0:13:53
0:13:53
 0:00:12
0:00:12
 0:00:11
0:00:11
 0:03:40
0:03:40
 0:04:26
0:04:26