filmov
tv
Area between two Parabolas | Area Under Curve Class 12 | Jee Mains Maths PYQ | #jee #maths #youtube

Показать описание
About this Video -
In this video we have discussed a Very GOOD concept Question of IIT JEE MAINS 2022 Area Under the Curve Chapter for IIT JEE. Asked in IIT JEE MAINS June 25, 2022, Shift-2. It is a very GOOD question based on fundamental concept. Here we will revise every aspect of the theory part related to the question. After seeing the video you will able to solve such problems very easily......
Question:
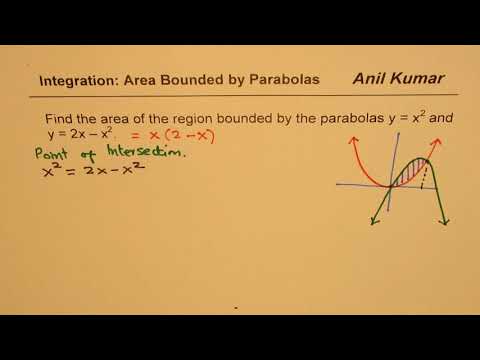
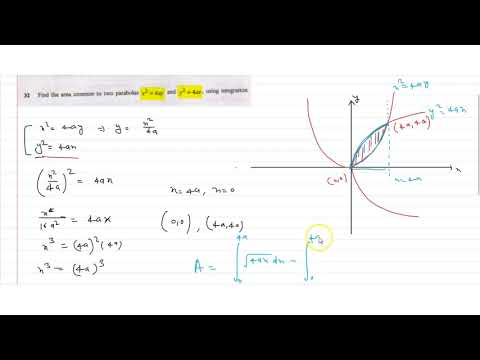
The area of the region enclosed between the parabolas y^2=2x-1 and y^2=4x-3 is
(A) 1/3 (B) 1/6 (C) 2/3 (D) 3/4
Ans: A [JEE Mains June 25, 2022; Shift-2]
NOTE : Please feel free to ask any doubt related from class 5 to class 12, IIT Advance and IIT Mains. We will definitely solve your doubt as soon as possible. Please Post your doubts in the comment box.
These videos are the very informative for all competitive examinations such as IIT JEE Advance, IIT JEE Mains, KVPY, Mathematics Olympiads and many more. You will be able to solve problems of IIT Advance and Mains by using the concept covered in the video.
Hi,
I am your Maths Guru. Welcome to my channel MathsBySm.
About this Channel -
Friends this channel is managed by very experienced IIT faculty and IITian. Friends here you will learn fundamental concepts and problem solving skills. Our moto is to provide coaching to all the students of class 11, class 12, IIT Aspirants, Olympiad, NDA and various other competitive examinations free of cost. Our aim is to provide basic and Advance level concepts to all those students who are willing to learn and not able to pay fee of reputed coaching institutes. Please watch the videos till the end to learn basic and Advance concepts. For doubt related to any topic in Mathematics, please write in the comment box.
#iit | #iitjee | #aryabhata | #jeemains | #jee | #pyq | #iitadvanced |
#problem | #problems | #tricks | #area | #areaoftriangle | #areaofparallelogram | #areaunderthecurve
In this video we have discussed a Very GOOD concept Question of IIT JEE MAINS 2022 Area Under the Curve Chapter for IIT JEE. Asked in IIT JEE MAINS June 25, 2022, Shift-2. It is a very GOOD question based on fundamental concept. Here we will revise every aspect of the theory part related to the question. After seeing the video you will able to solve such problems very easily......
Question:
The area of the region enclosed between the parabolas y^2=2x-1 and y^2=4x-3 is
(A) 1/3 (B) 1/6 (C) 2/3 (D) 3/4
Ans: A [JEE Mains June 25, 2022; Shift-2]
NOTE : Please feel free to ask any doubt related from class 5 to class 12, IIT Advance and IIT Mains. We will definitely solve your doubt as soon as possible. Please Post your doubts in the comment box.
These videos are the very informative for all competitive examinations such as IIT JEE Advance, IIT JEE Mains, KVPY, Mathematics Olympiads and many more. You will be able to solve problems of IIT Advance and Mains by using the concept covered in the video.
Hi,
I am your Maths Guru. Welcome to my channel MathsBySm.
About this Channel -
Friends this channel is managed by very experienced IIT faculty and IITian. Friends here you will learn fundamental concepts and problem solving skills. Our moto is to provide coaching to all the students of class 11, class 12, IIT Aspirants, Olympiad, NDA and various other competitive examinations free of cost. Our aim is to provide basic and Advance level concepts to all those students who are willing to learn and not able to pay fee of reputed coaching institutes. Please watch the videos till the end to learn basic and Advance concepts. For doubt related to any topic in Mathematics, please write in the comment box.
#iit | #iitjee | #aryabhata | #jeemains | #jee | #pyq | #iitadvanced |
#problem | #problems | #tricks | #area | #areaoftriangle | #areaofparallelogram | #areaunderthecurve
Комментарии
 0:03:30
0:03:30
 0:05:59
0:05:59
 0:07:52
0:07:52
 0:10:28
0:10:28
 0:11:25
0:11:25
 0:48:59
0:48:59
 0:11:47
0:11:47
 0:07:36
0:07:36
 0:22:58
0:22:58
 0:05:35
0:05:35
 0:12:27
0:12:27
 0:07:35
0:07:35
 0:00:32
0:00:32
 0:00:51
0:00:51
 0:04:57
0:04:57
 0:07:23
0:07:23
 0:04:51
0:04:51
 0:06:47
0:06:47
 0:00:16
0:00:16
 0:07:09
0:07:09
 0:13:42
0:13:42
 0:12:30
0:12:30
 0:03:28
0:03:28
 0:18:02
0:18:02