filmov
tv
Leibniz' rule: Integration via differentiation under integral sign

Показать описание
I discuss and solve an example where, given a simpler integral, a more complicated integral is evaluated through differentiation. The method features an application of Leibniz' rule for differentiating an integral. Such an example is seen in 2nd-year university mathematics.
The Leibniz rule for integrals: The Derivation
Leibniz' rule: Integration via differentiation under integral sign
Leibniz's Integral Rule
Leibniz integral rule
Leibniz Rule of Integration / Feynman Integration (General Case)
Leibniz's Rule - 12 Integrals, Ep. 4
Evaluating challenging integrals via differentiation: Leibniz rule
Material derivative and Leibniz rule
L-12 TOTAL DERIVATIVE | TOTAL DIFFERENTIATION | CHAIN RULE | ENGINEERING MATHEMATICS | TYPE-1, 2 &am...
Differentiate under integral signs: Leibniz rule
chapter two Differentiating Any Integral Leibniz Rule
Using leibniz rule to find the 6th derivative of a function Problem 12-5-3
What is Leibniz rule with Example 1
Leibniz Integral Rule Quiz
Leibniz's Rule (Part 1): Diff under Int Sign
Differentiation under integral signs: Leibniz rule
Leibniz's Derivative Notation (1 of 3: Overview)
Feynman's integration trick: Differentiating under the Integral sign | Leibniz Rule
Using Leibniz rule to find nth derivative problem 12-3-1
How REAL Men Integrate Functions
Fundamental Theorem of Calculus Part 1
Differentiation Of Integrals Leibniz Rule // Differentiation Under the Integral Sign
Differentiation under the Integral Sign Tutorial
Leibniz Integral Rule | Lecture 1 | General formula proof of differentiation under integral sign
Комментарии
 0:17:40
0:17:40
 0:04:43
0:04:43
 0:09:25
0:09:25
 0:22:46
0:22:46
 0:05:56
0:05:56
 0:08:03
0:08:03
 0:05:11
0:05:11
 1:09:47
1:09:47
 0:10:48
0:10:48
 0:16:35
0:16:35
 0:06:36
0:06:36
 0:09:51
0:09:51
 0:15:24
0:15:24
 0:03:26
0:03:26
 0:40:35
0:40:35
 0:13:10
0:13:10
 0:21:56
0:21:56
 0:06:44
0:06:44
 0:00:35
0:00:35
 0:11:30
0:11:30
 0:10:44
0:10:44
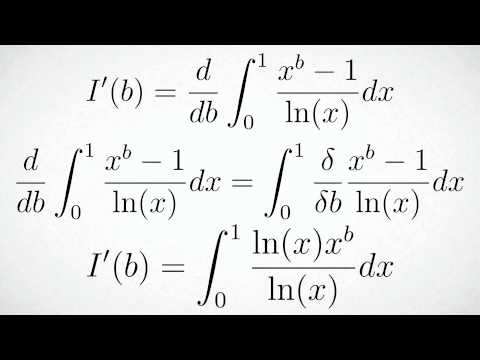 0:08:21
0:08:21
 0:12:59
0:12:59