filmov
tv
Algebraic numbers are countable
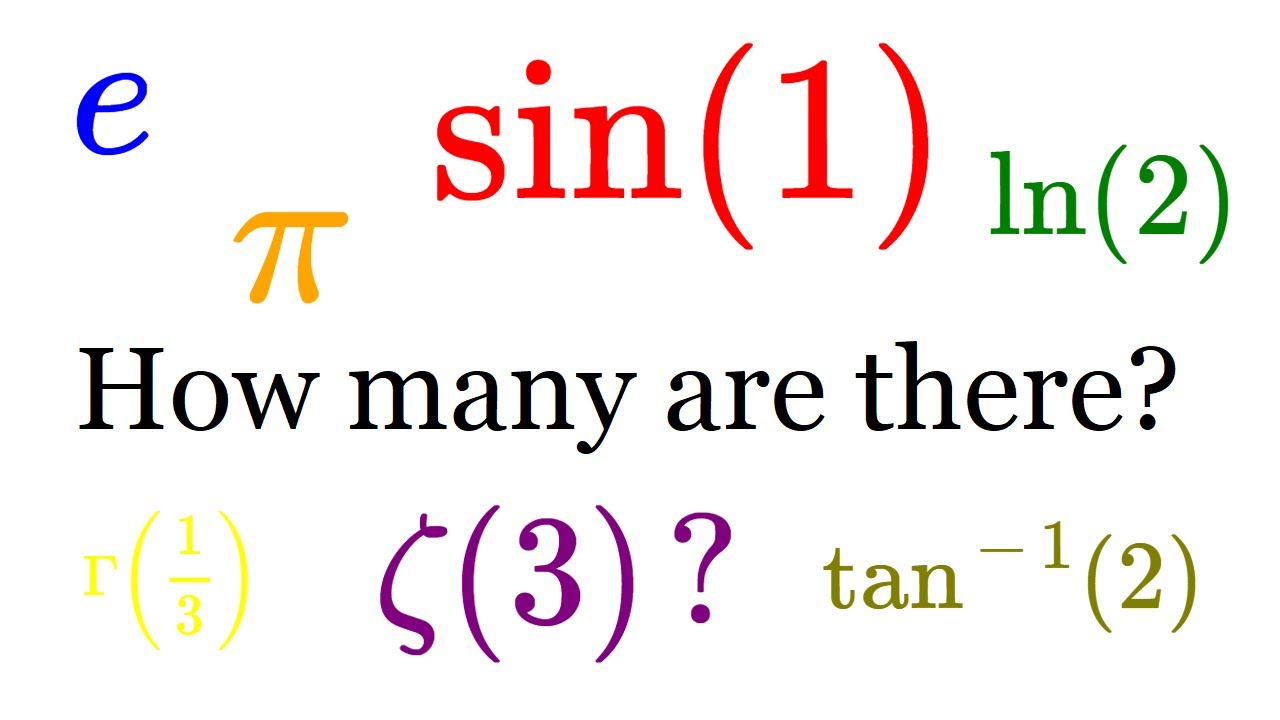
Показать описание
Transcendental numbers are uncountable, algebraic numbers are countable.
There are two kinds of real numbers: The algebraic numbers (like 1, 3/4, sqrt(2)) and the transcendental numbers (like pi or e). In this video, I show that the algebraic numbers are countable, which means that there are so many transcendental numbers that if you choose a real number at random, the probability that it's transcendental is 1!!! This is so suprising, because we're much more used to dealing with algebraic numbers!
Note: My apologies for not making my usual outro at the end, my phone ran out of battery, but luckily it caught most of the video!
There are two kinds of real numbers: The algebraic numbers (like 1, 3/4, sqrt(2)) and the transcendental numbers (like pi or e). In this video, I show that the algebraic numbers are countable, which means that there are so many transcendental numbers that if you choose a real number at random, the probability that it's transcendental is 1!!! This is so suprising, because we're much more used to dealing with algebraic numbers!
Note: My apologies for not making my usual outro at the end, my phone ran out of battery, but luckily it caught most of the video!
Algebraic numbers are countable
Algebraic numbers are countable
AKPotW: Algebraic Numbers are Countable [Algebra]
Two Countable Sets
Baby Rudin Chapter 2, Problems 2 and 3 (algebraic numbers and countability)
The set of all algebraic numbers is countable. So, there exist real transcendental numbers over Q
Section 5 2-5.5, part 14 Algebraic and transcendental numbers
Define Algebraic number Show that of algebraic numbers is countable || Set theory #tmbuuniversity
Math 10th Class|EX#5.2|Q#3,4|De-Morgan's law
Ordinals vs Cardinals (and how many algebraic numbers are there?)
FIT2.3.1. Algebraic Numbers
Algebraic Numbers, Countability, & Equinumerosity – L16 Comp. Sci. 230 - Bruce Donald, Duke Univ...
Algebraic Numbers
Algebraic numbers and number fields
Lecture 1.3 - Rational and Algebraic Numbers
👉COUNTABLE SET 🌟
Algebraic Numbers and transcendental Numbers 🔥🔥
Counting Polynomials & Transcendental, Algebraic No.s | Real Analysis |MSc |DU |ISI |BHU | IIT ...
Algebraic Numbers
Lecture 4 Algebraic numbers
Field Theory -- Qbar, the field of algebraic numbers -- Lecture 8
Rational Numbers are Countable
math numbers 09 Algebraic Numbers Transcendental Numbers
MAT302 U-1 Algebraic Numbers and Cantor set Construction
Комментарии
 0:04:21
0:04:21
 0:13:00
0:13:00
 0:03:21
0:03:21
 0:00:55
0:00:55
 0:10:30
0:10:30
 0:02:43
0:02:43
 0:12:33
0:12:33
 0:05:31
0:05:31
 0:15:13
0:15:13
 0:10:18
0:10:18
 0:13:22
0:13:22
 1:07:24
1:07:24
 0:12:19
0:12:19
 0:17:49
0:17:49
 0:21:25
0:21:25
 0:00:06
0:00:06
 0:06:03
0:06:03
 0:18:37
0:18:37
 0:00:20
0:00:20
 0:17:38
0:17:38
 0:10:30
0:10:30
 0:04:44
0:04:44
 0:14:46
0:14:46
 0:41:21
0:41:21