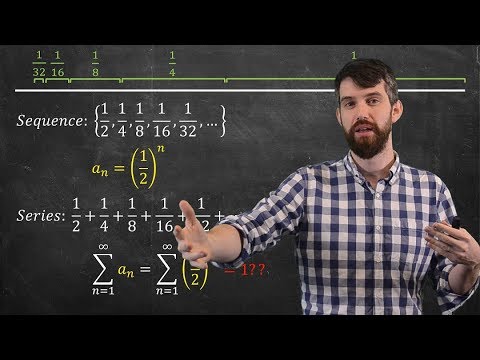
Intro to Series: What is 1/2+1/4+1/8+1/16+...?

A series is the infinite sum of the terms of a sequence. In this video we see some examples, introduce the terminology, and then give the formal definition of convergence of a series in terms of partial sums.

****************************************************
YOUR TURN! Learning math requires more than just watching videos, so make sure you reflect, ask questions, and do lots of practice problems!
****************************************************

****************************************************
Other Course Playlists:

***************************************************

► Want to learn math effectively? Check out my "Learning Math" Series:

►Want some cool math? Check out my "Cool Math" Series:

*****************************************************

*****************************************************

*****************************************************

This video was created by Dr. Trefor Bazett, an Assistant Professor, Educator at the University of Cincinnati.

BECOME A MEMBER:

MATH BOOKS & MERCH I LOVE:

[jordanr]

great explanation professor, thank you!

[icebearreal]

Excellent Explanation, I am using your videos to teach myself calculus 2 alongwith the Stewart Calculus book.

[christaylor]

One way to define precisely what a number series is, is to say that it's an ordered pair (q, sums(q)) of number sequences, where sums(q) is the sequence of partial sums of q. The sum-value of such a series is 0 if q is empty, is the last sum in sums(q) for a finite non-empty q, is the limit of sums(q) if q is infinite and converges, and is undefined if sums(q) is infinite and does not converge.

In standard Sigma notation, the expression Sigma q is used both to represent the series itself, but also its sum-value, if the series converges. So e.g. Sigma q = 1 for infinite q actually means that the series Sigma q =(q, sums(q)) converges and has the sum-value 1.

[hmasamuneeric]

I just realized the more fractions you put, the closer you get to 1. That’s how I got 1.

[maimonida]

my 7 years old son ask me this question today ...thank you for the explanation

[jamestagge]

though this is NOT relevant to your video, i thought it would be well within your understanding that you might be willing to comment. This is something i have been thinking about and it addresses the use of concepts as a context for launching mathematical theories/formulae but seems to always be conceptually contradictory. have a line segment 1” long and consider the claim that it is composed of infinite points, none of which can be defined in terms of scope or dimension (or they could not be infinite in number). What if I can show that this is not the case?
The line segment has two ends where it terminates. Those ends, whether theoretical or graphically displayed, by definition are demarcated each by a point, part of those of which the line segment is composed. Beyond those two points in the respective directions away from the two ends, there cannot be additional points or the line segment ends/terminations could not be defined. So, we know then that the last point must be that by which each end is terminated. Now each end of the line segment is a very particular location in space, each to the other and must be definitively demarcated that there might be that termination or a line segment at all. If that is so, it demands that some aspect of these end points be asserted that each end of the line segment is defined by them. For example, it could not be the center of the points (which is not supposed to be defined or the point would have scope and dimension) or the distance from that center to the outside edge would mean that the line segment was actually longer than demarcated. So, the end of the line must be by definition, defined by the outside edge of each of those points, by which there must be a side opposite and thus a middle. Therefore, these points necessarily have scope and dimension and there cannot be an infinite number of them along that line segment.
Here, it is the logic of the means of defining the line segment to begin with/at all which must be contradicted to claim that there are infinite points along its finite length and that clearly cannot be so. We cannot define a proposition which denies the very means of its presentation.
So, what do you think?

[manfredwilczek]

Warum wird nicht ins deutsche übersetzt sondern nur in englisch
?

[creativeminds]

Hi, from india

Where to get the font you have used

It is used in our jee advanced

[robertobastardo]

Actually there's nothing special about a convergent series, while watching your video I realized that as you divide by a greater number in relation to the last generated value of the sequence would be like counting backwards in a cyclical way, for example i can say :

a) 2 + 1/2 + 1/4 + 1/8 + 1/16 ... < 3
b) 3 + 1/3 + 1/9 + 1/27 + 1/81 ...< 4

Also the numerator doesn't have to be 1, it can be any number lower or equal than the first whole number of the series, for example:

c) 5 + 5/25 + 5/125 + 5/625 ...< 6

Also as long as you're generating the next number by dividing the previous number by any number greater than 2 you will always have the same kind of behavior, for example:

d) 3 + 3/9 + 3/ (9*2) + 3/(18*3) + 3/(54*5) + 3/(270*2) ...< 4

I call this Regressive Cyclical Counting.

[gezzuzzful]

the sum of an infinity number of a positive number is infinity

[wakeawake]

Please help me, how can I solve an equation like:- 2^x = 3x^2 + 2x + 1. In this equation how can I find the value of x? Please reply🙏🙏🙏