Calculating Speed (Metric Units)

The things around us move in different ways. When something is moving, we say it is in motion. An object is in motion when it is continually changing position in relation to other objects. We can describe motion in different ways.

You can describe the motion of a child on a swing as a back and forth motion. The people on a carousel move round and round. An airplane is in motion as it moves down a runway. It moves in a straight line, then up into the air.

Along with describing motion, there are many aspects of motion that can be measured. One way we measure motion is speed. Speed describes how fast or slow something is moving. It describes the distance an object travels in a certain time. To measure the speed of something, you need to know two things: how far it traveled, and how long it took to travel that far.

Let's look at some common examples:

meters per second (m/s)

A sprinter running a 100-meter dash finishes the race in 10 seconds. To calculate the speed, we divide the distance, which is 100 meters, by the time, 10 seconds. This gives us a speed of 10 meters per second. So, the sprinter's speed is 10 meters per second.

Next, consider a car in a drag race. It covers a distance of 400 meters in 20 seconds. To find the speed, we divide the 400 meters by the 20 seconds. The result is a speed of 20 meters per second, indicating the car's rapid movement.

Finally, let's look at a swimmer in a pool. The swimmer completes a 50-meter lap in 25 seconds. By dividing the distance, 50 meters, by the time, 25 seconds, we calculate the speed to be 2 meters per second. This shows the swimmer's pace as they move through the water.

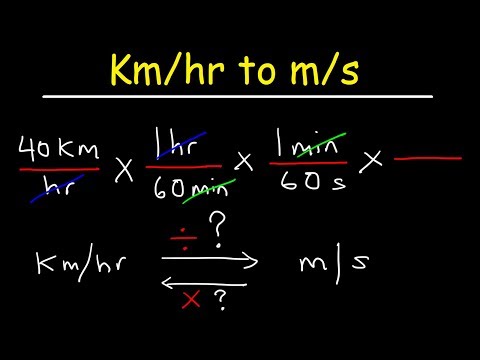
We can also measure speed in kilometers per hour (km/h), a unit commonly used for longer distances and over longer time periods.

Consider a cyclist on a long-distance ride. They cover a distance of 40 kilometers in 2 hours. To calculate their speed, we divide the distance traveled, 40 kilometers, by the time taken, which is 2 hours. This results in a speed of 20 kilometers per hour, indicating a steady pace over a considerable distance.

Next, think about a train journey. The train travels 300 kilometers in 3 hours. To find the speed, we divide the 300 kilometers by the 3 hours. The calculation gives us a speed of 100 kilometers per hour, a reflection of the train's efficient long-distance travel.

Lastly, let's look at a leisurely boat trip. The boat travels 90 kilometers in 6 hours. By dividing the distance, 90 kilometers, by the time, 6 hours, we find that the boat's speed is 15 kilometers per hour. This slower speed is typical for a relaxed, scenic boat journey.

In conclusion, understanding speed in both meters per second and kilometers per hour allows us to appreciate the varying paces of different objects and activities around us. Whether it's the swift dash of a sprinter, the steady journey of a long-distance cyclist, or the serene glide of a boat, speed is a fundamental aspect of motion that helps us quantify and understand how the world moves.