A Random Number Paradox (Part 1)

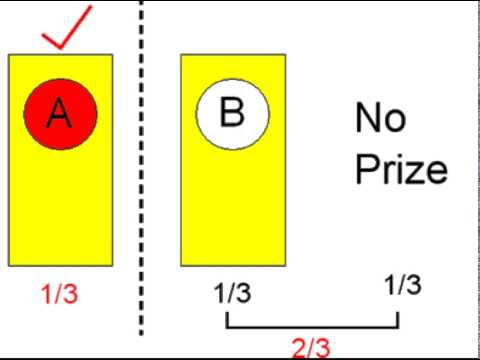
In this short, I talk about an interesting number paradox about random numbers that I've heard before. Stay tuned next week for part 2, which will make things even more confusing!

Patreon Supporters:
Christoph Kovacs
David Johnston
Jason Killian
p11
Richard Penner
Rosario
trb

[QuantSpazar]

You can't pick a random natural number with uniform probability

[hydraslair]

You can't define a uniform probability over the naturals.

[steffahn]

Video: "Pick a random natural number"
Me: "What’s the probability distribution?"

[davidgillies]

This is one of those things where if you don't know the resolution of the paradox you have to be very very clever to deduce it but if you've done an elementary course on measure theory you know the answer immediately.

[mariomascolo]

If you claim that 42 is less than any random natural number with probability one, you have implicitly defined a probability measure - on P(N) - which assigns measure 0 to finite sets (i.e. numbers smaller than 42) and measure 1 to countable sets (i.e. numbers bigger than 42). This contradicts the sigma-additivity of your measure (a countable union of disjoint sets of measure zero must have measure zero), which therefore is not a measure at all, much less a probability measure.

[YitzharVered]

Theres no measure on the natural numbers that allows a uniform distribution.

[systemicio]

Many paradoxes is either self-referential, infinity or ambiguity. One can argue the infinity also self-referential since the infinity constructed using recursion.

[lih]

I guess that's why people don't use probabilities on infinite sets like that, bad math, bad logic?

[aza-joru]

I think that the problem lies in the fact that "42 is almost surely less than any number" this "almost surely" is wrong because we are not in the continuous case, and the probability of a singleton is not necessarily 0. For example we can define P(X=k)=1/2^k and in this case P(X<42)is not zero.

[berry]

It's not a paradox. it's just wrong conclusions which you might find "obvious". like those many 1=0 proofs

[putyavka]

If you make a uniform mapping of infinite range of number to unit range then any 2 finite number will be infinitly close to 0 and equal each other. And 0 less then any other number in range from 0 to 1. So no paradox

[onebronx]

"less than ALMOST ALL" != "less than ANY"

[jakobr_]

What’s going on is that things can still happen even when the probability of them not happening is 1. Like the probability of hitting any single point on a dart board.

Also these two events are not independent

[gabitheancient]

ig the problem is assuming 100% probability is the same as guaranteed trying to use an uniform distribution in an infinite set

[BleachWizz]

This proves one number is 100% of the time smaller than the other. seem fine for me ;p

[dzuchun]

probability 1 does not mean "certain yes", as well as probability 0 does not mean "certain no"

the reason is, probability of you picking 42 is 0, but you've surely just did that

[arthurreitz]

No paradox
Numbers don't exist 🙃

[franks.]

“It depends on what the meaning of the word ‘is’ is.” (William Jefferson Clinton)
42 gave it away. Either that or something about measure theory for probabilities.

[ScreamingManiac]

Not a paradox, just a consequence of selectively using different mathematical concepts at will.