filmov
tv
Easiest way to solve this Olympiad problem || Trigonometry || Math Olympiad
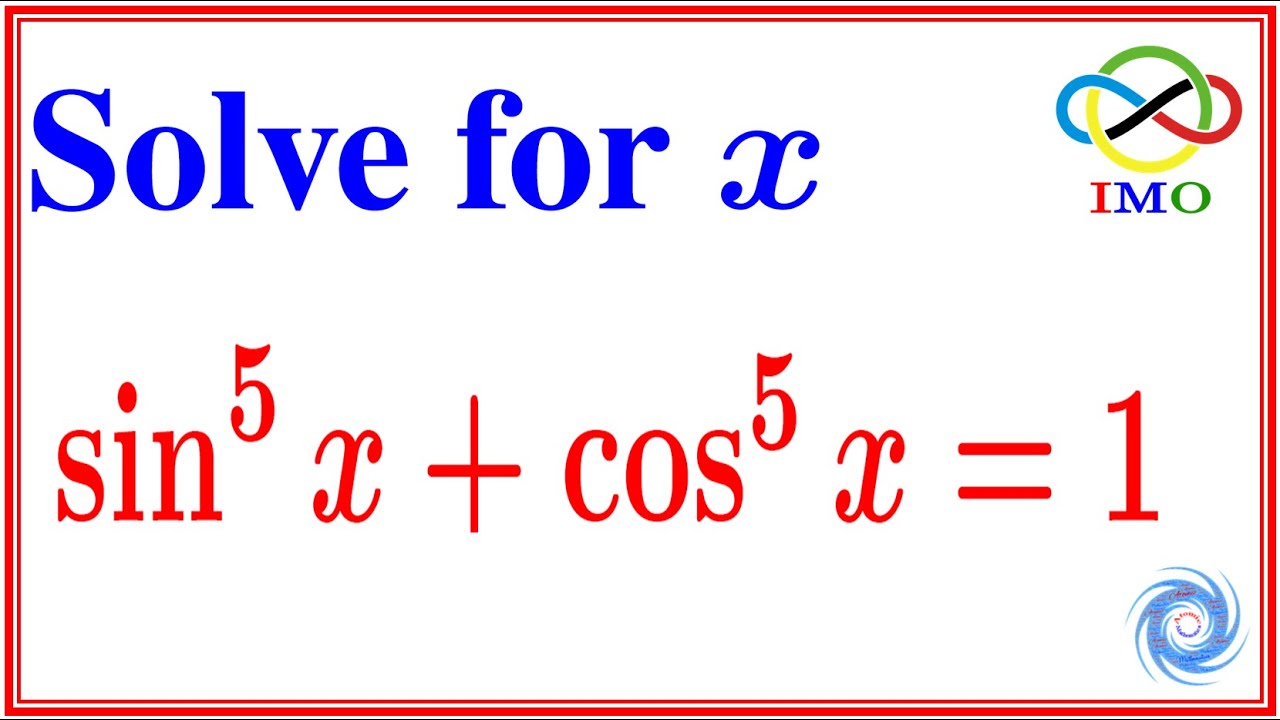
Показать описание
In this series, we will regularly update brainstorming problems in mathematics. The collection of problems will be taken from Algebra, Calculus, Mathematical Reasoning, Probability, Number Theory, Functional Analysis, etc.
Subscribe our channel to get regular update. Thank you.
How to Solve the Rubik’s Cube Fast & Easy!
How to solve a Rubik’s Cube in under 30 seconds
This 3 second Rubik’s cube solve is INSANE 😯
How To Solve A 3x3 Rubik's Cube Using Only 2 Moves (Really Works)!
Learn How to Solve a Rubik's Cube in 10 Minutes (Beginner Tutorial)
Easy Tips And Tricks to Solve 3x3 Rubik's Cube in Under 1 Minute!
The EASIEST Way To Solve the 3x3 Rubik's Cube! - Beginners Method Tutorial
How fast can you solve a Rubik’s Cube?? 🤔
How to Solve a 3x3 Rubik's Cube [With Example Solve]
How to ACTUALLY Solve A Rubik's Cube In 5 Seconds
How to solve a Rubik’s cube | The Easiest tutorial | Part 1
BEST WAY to solve this QUADRATIC EQUATION
Easiest Solve For a Rubik's Cube | Beginners Guide/Examples | STEP 1
How to Solve the Rubik's Cube FASTER with the [Beginner Method]
Can you solve this equation?
HOW BEGINNERS SOLVE THE RUBIK’S CUBE
How to Solve a Rubik's Cube | WIRED
HOW TO SOLVE A RUBIK'S CUBE (& Remember The Steps!)
How To Solve a 2x2 Rubik's Cube | Simple Method
This is How I Solve a Rubik's Cube in UNDER 10 Seconds...
How To Solve The 3x3 Faster (CFOP Method)
Can you solve a 4 move scramble? | NEXcube
Solve a 3x3 Rubik's Cube In a Few Minutes | Beginner's Guide Step By Step
How to Solve a Rubik's Cube (Easiest Way)
Комментарии
 0:08:01
0:08:01
 0:00:45
0:00:45
 0:00:35
0:00:35
 0:01:15
0:01:15
 0:10:03
0:10:03
 0:06:38
0:06:38
 0:15:38
0:15:38
 0:00:18
0:00:18
 0:19:47
0:19:47
 0:09:16
0:09:16
 0:12:55
0:12:55
 0:12:40
0:12:40
 0:07:59
0:07:59
 0:11:22
0:11:22
 0:00:28
0:00:28
 0:01:00
0:01:00
 0:24:12
0:24:12
 0:18:12
0:18:12
 0:06:33
0:06:33
 0:14:52
0:14:52
 0:09:02
0:09:02
 0:00:34
0:00:34
 0:10:01
0:10:01
 0:11:38
0:11:38