filmov
tv
Differential Equations with Forcing: Method of Variation of Parameters

Показать описание
This video solves externally forced linear differential equations with the method of variation of parameters. This approach is extremely powerful. The idea is to solve the unforced, or "homogeneous" system, and then to replace the unknown coefficients c_k with unknown functions of time c_k(t), and then solve for these functions based on the external forcing.
@eigensteve on Twitter
This video was produced at the University of Washington
%%% CHAPTERS %%%
@eigensteve on Twitter
This video was produced at the University of Washington
%%% CHAPTERS %%%
Differential Equations with Forcing: Method of Variation of Parameters
Differential Equations with Forcing: Method of Undetermined Coefficients
Systems of Differential Equations with Forcing: Example in Control Theory
Undetermined Coefficients: Solving non-homogeneous ODEs
Differential Equations Ch5, Forcing function
3.6 part 4: Modeling Forced Damped Oscillations using Differential Equations
solving equations with discontinuous forcing functions -- differential equations 20
Differential Equation | Piecewise forcing function example
Differential equations, a tourist's guide | DE1
Method of Undetermined Coefficients - Nonhomogeneous 2nd Order Differential Equations
This is why you're learning differential equations
5.6 Differential Equations with Discontinuous Forcing Functions
exploring different forcing functions -- differential equations 12
Differential Equations. All Basics for Physicists.
Undetermined Coefficients With Different Forcing Functions -- Differential Equations Examples #12
Physics Students Need to Know These 5 Methods for Differential Equations
Differential Equations | Laplace Transform of a Piecewise Function
undetermined coefficients with first order linear DEs
4 Types of ODE's: How to Identify and Solve Them
Class-71:LTI Systems-Differential equations solving for forced response
How to solve differential equations with forcing term (linear difeq video 10)
Method of Undetermined Coefficients
Mixing Salt and Water - First Order Differential Equations
Drag Force Differential Equation
Комментарии
 0:23:25
0:23:25
 0:20:09
0:20:09
 0:16:04
0:16:04
 0:12:44
0:12:44
 0:11:49
0:11:49
 0:08:00
0:08:00
 0:32:39
0:32:39
 0:07:53
0:07:53
 0:27:16
0:27:16
 0:41:28
0:41:28
 0:18:36
0:18:36
 0:12:31
0:12:31
 0:40:53
0:40:53
 0:47:38
0:47:38
 0:17:19
0:17:19
 0:30:36
0:30:36
 0:04:44
0:04:44
 0:13:50
0:13:50
 0:06:57
0:06:57
 0:14:48
0:14:48
 0:19:08
0:19:08
 0:16:32
0:16:32
 0:11:49
0:11:49
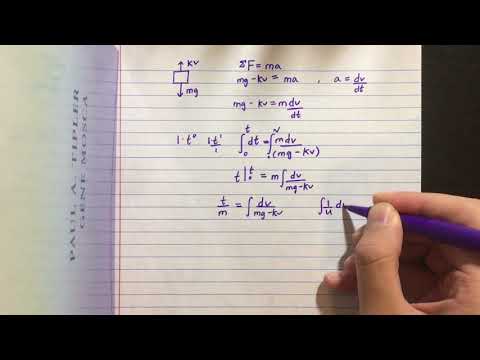 0:10:51
0:10:51