Binomial Heap

#techlearners
Introduction to binomial Heap and operations on binomial heap.
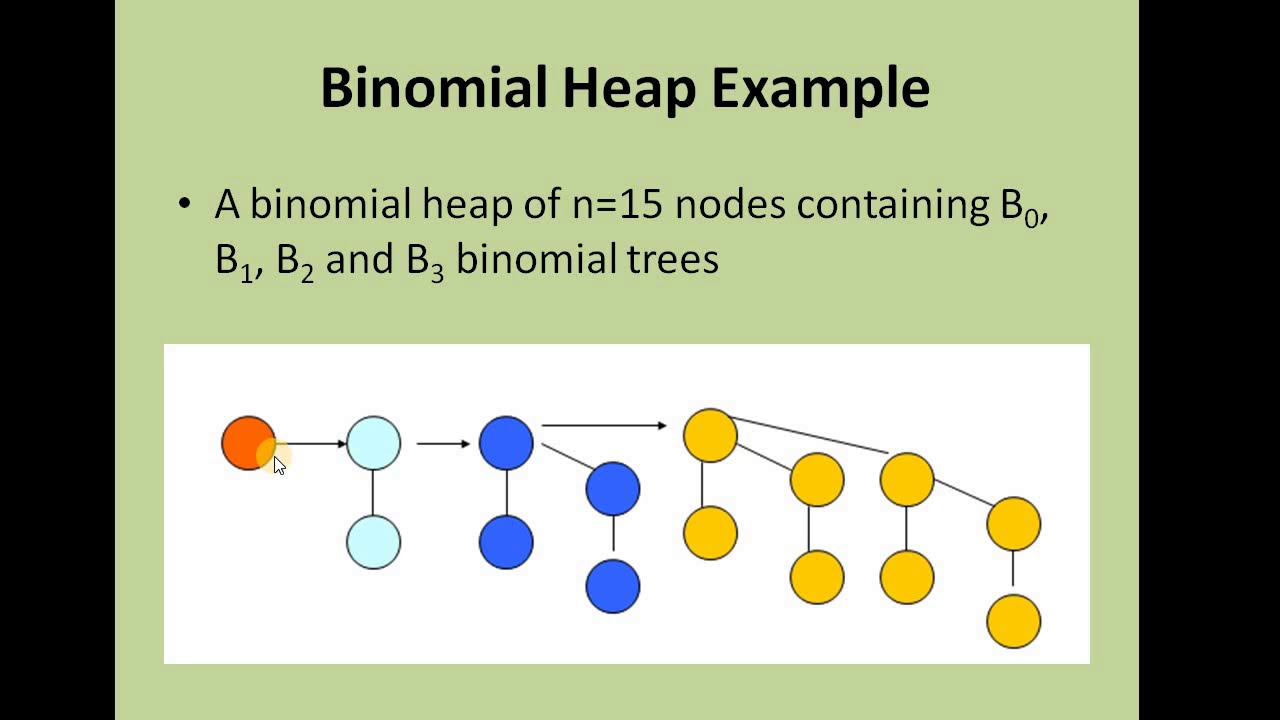
Binomial Heap is a collection of binomial trees
that satisfies the following properties
No two binomial trees in the collection have the same size
Each node in the collection has a key
Each binomial tree in the collection satisfies the heap order property
Roots of the binomial trees are connected and are in increasing order
or
A binomial heap H is a set of binomial trees
that satisfies the following binomial-heap
properties.

1. Each binomial tree in H obeys the min-heap property: the key of a node is greater than or equal to the key of its parent. We say that each such tree is min-heap-ordered.
2. For any nonnegative integer k, there is at most one binomial tree in H whose root has degree k.
Operations on Binomial Heap
Creation
Finding Minimum Key
Union
Insertion
Removal of the root of a tree
Decrease Key
Deletion

TECHLEARNERS BY NEERAJ SAXENA

[Moonz]

At 5:10, it should be 2^k nodes not 2k nodes for binomial tree Bk.
Thanks for the video.

[JackAdrianZappa]

09:18 roots of the binomial trees are connected and are in increasing
Yet at 10:15, you show a binomial whos roots are not in increasing order.

[PKSon-ijlh]

You are making conceptual mistakes. At 5:40, 6 does not have degree 1. It has degree 0.No of nodes is not 2k, It is 2^k. So, for k=3, binomial tree will have 8 nodes (2^3). At 9:24 and 10:08, "Roots of binomial trees are connected and in increasing order".At 10:14, in the diagram you show, the connected roots are not in increasing order. If you do not wish to do it diligently, may as well not do it.

[BelegaerTheGreat]

If I didn't already know what Binomial Heaps are, this video would have been very damaging to my understanding.

[StoneAge]

you have not discuss Application of binomial heap which you say that you will discuss at 0 : 36