filmov
tv
How to check if two given line segments intersect? | GeeksforGeeks

Показать описание
This video is contributed by Siddharth Chandra
Please Like, Comment and Share the Video among your friends.
Also, Subscribe if you haven't already! :)
How to check if two given line segments intersect? | GeeksforGeeks
Simple Algorithm to Check if Two Strings are Permutations | Beginner Level
How to Check if Two Lists are Equal in Python
Check if two line segments intersect
Frequently Asked Java Program 16: How To Check The Equality Of Two Arrays
How to Check if Two Values are Equal in Excel
How to check if two files are identical, within a Windows shell script?
to check Whether the given two numbers are equal or not
Check If Two Arrays Are Equal Or Not | C Programming Example
Check if two binary trees are identical (Algorithm/code/program)
Leetcode - Check If Two String Arrays are Equivalent (Python)
Check if two strings are anagrams
What is the simplest way to check if two images are the same?
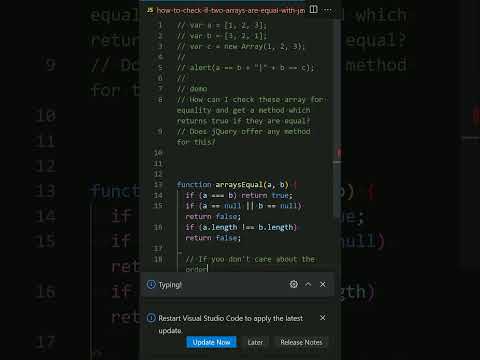
How to check if two arrays are equal with JavaScript?
Check if two strings are anagrams
Check if two binary trees are identical (Algorithm/code/program)
PYTHON : How does a Python set([]) check if two objects are equal? What methods does an object need
15.Check if two arrays are equal or not | Hashing | Python | GFG | Must Do Coding Questions
How to check if two arrays are equal or not in C++
How to check if Two Strings are Anagrams in Python
How to Check if Two Strings are Permutations of Eachother
C Program To Check If Two Numbers are Co-Prime or Not
How to check if two lists contain overlapping elements in Elixir
How to check if a value is between two values in Excel
Комментарии
 0:03:07
0:03:07
 0:14:06
0:14:06
 0:01:00
0:01:00
 0:12:06
0:12:06
 0:09:58
0:09:58
 0:01:11
0:01:11
 0:01:37
0:01:37
 0:00:41
0:00:41
 0:05:41
0:05:41
 0:09:21
0:09:21
 0:05:39
0:05:39
 0:08:50
0:08:50
 0:01:12
0:01:12
 0:00:38
0:00:38
 0:09:07
0:09:07
 0:07:34
0:07:34
 0:01:16
0:01:16
 0:02:57
0:02:57
 0:02:29
0:02:29
 0:01:46
0:01:46
 0:15:19
0:15:19
 0:04:38
0:04:38
 0:00:59
0:00:59
 0:01:23
0:01:23