filmov
tv
Riemann Integration- If f,g are Riemann integral then f/g is also Riemann integral. Lecture 28
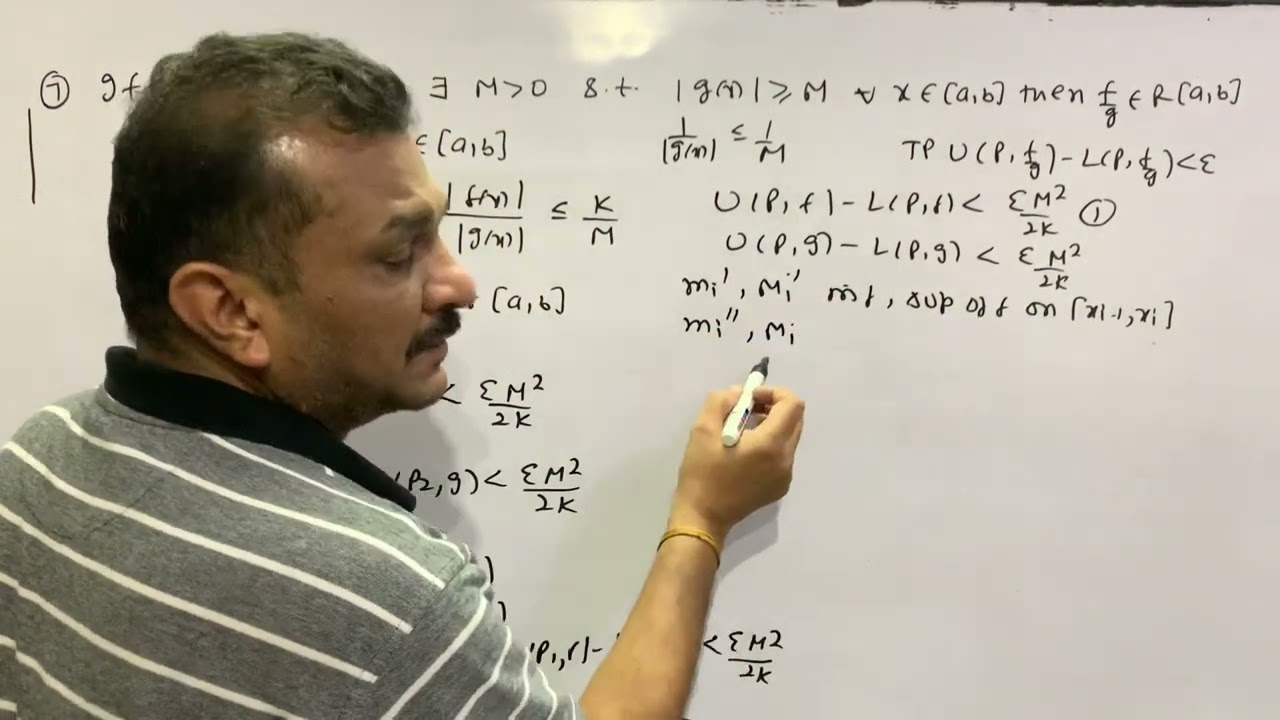
Показать описание
0:13:36
Riemann Integration- If f and g are Riemann integral then fg is Riemann integral.Lecture-26
0:49:02
(RA17) Riemann Integrability
0:09:02
Riemann Integration- If f,g are Riemann integral then f/g is also Riemann integral. Lecture 28
0:09:51
Riemann Integration | Lecture 27 | Square of Riemann Integrable Function is Riemann Integrable
0:15:19
Riemann Integration-If f and g are Riemann integral then f + g is Riemann integral. Lecture-25
0:18:40
Riemann Integration | Lecture 28 | Sum of Two Riemann Integrable Functions is Riemann Integrable
0:07:18
Riemann Integration- If f is Riemann integral then 1/f is also Riemann integral.Lecture 27
0:08:24
Riemann Integration | Lecture 11 | Example of non Integrable Function
0:11:41
f, g are riemann integrable then f+g also Riemann iintegrable 4th sem u-5
0:13:11
Riemann Integration | Lecture 26 | Modulus of Riemann Integrable Function is Riemann Integrable
0:19:11
15. Properties of the Riemann integral - Constant multiple of an integrable function is integrable
0:20:27
Properties of the Riemann integral
1:11:15
Lecture 15: Riemann Integral Contd..
0:08:01
Theorem || if f and g are bounded function on [a,b] || riemann integral || bsc msc mathematics
0:20:45
mod02lec17 - Connecting the Jordan measure with the Riemann integral - Part 1
0:12:37
Properties of Riemann integral -2
0:06:34
#Important theorem on Riemann Integration | #Real Analysis | #OU | #KU | #PU | #TU | #MGU
![If f∈R[a,b]](https://i.ytimg.com/vi/FCiX_tluZSI/hqdefault.jpg)
0:19:22
If f∈R[a,b] ,g∈R[a,b] and |g(x)| greater than 0 then f/g∈R[a,b] #bsc #math #riemannintegral
![If f∈R[a,b] ,](https://i.ytimg.com/vi/dVTRKuwjsTo/hqdefault.jpg)
0:22:12
If f∈R[a,b] , g∈R[a,b] then f±g∈R[a,b] and ∫_a^b (f±g)=∫_a^b (f) ± ∫_a^b (g) #riemannintegral...
0:20:56
Riemann-Stieltjes Integrals Theorems and Corollary , Real Analysis - ||
0:05:23
REAL ANALYSIS,if f,g is reimaan integrable then prove that fg is also reimaan integrable. Lec no 19
![If f∈R[a,b] ,](https://i.ytimg.com/vi/cqMe2GG9b2A/hqdefault.jpg)
0:19:16
If f∈R[a,b] , g∈R[a,b] then fg∈R[a,b] || Real Analysis || Riemann Integral #educationhelp
0:24:32
mod02lec18 - Connecting the Jordan measure with the Riemann integral - Part 2
0:20:45
Connecting the Jordan measure with the Riemann integral - Part 1
Комментарии