filmov
tv
A.2.7 Множества

Показать описание
#dudvstud #математиканапальцах #войтивайти
Рассматриваем новое явление: множество. Это одно из ключевых понятий математики. Рассматриваем классификацию множеств и способы их определения.
Рассматриваем новое явление: множество. Это одно из ключевых понятий математики. Рассматриваем классификацию множеств и способы их определения.
A.2.7 Множества
9 класс, 2 урок, Множества и операции над ними
Множества и операции над ними
Множество. Элементы множества. 5 класс.
Выписать подмножества множества
Множества чисел | Натуральные, целые, рациональные, иррациональные, действительные числа...
Подмножество множества
C++ 7 Множество
Торическая топология, комбинаторика и теория гомотопий, Лекция 7...
УРОК 05. Множества (7 класс)
Понятие множества. Способы задания множеств
Теория множеств. Мощность множества. Математика за минуту #shorts...
МНОЖЕСТВО И ЕГО ЭЛЕМЕНТЫ // ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ...
Понятие Множество
Множества. Объяснение для детей. Часть 7. Диаграммы Венна и круги Эйлера...
0+2=7 Одна головоломка, множество решений
Математика 4 класс. Решение неравенства. Множество решений...
Множество. Элементы множества. Пустое множество
#7 — Множество. Элемент множества [Математика, 1 класс]
Круги Эйлера. Логическая задача на множества. Иностранные языки...
Пересечение и объединение множеств (видео 1) | Множество | Алгебра...
Теория множеств. Что такое множество
задание множества
Изучаем математику с нуля / Урок № 16 / Множество
Комментарии
 0:11:30
0:11:30
 0:06:38
0:06:38
 0:05:46
0:05:46
 0:09:34
0:09:34
 0:02:11
0:02:11
 0:02:47
0:02:47
 0:02:31
0:02:31
 0:13:42
0:13:42
 1:36:24
1:36:24
 0:08:08
0:08:08
 0:17:04
0:17:04
 0:00:59
0:00:59
 0:05:49
0:05:49
 0:07:58
0:07:58
 0:01:01
0:01:01
 0:03:12
0:03:12
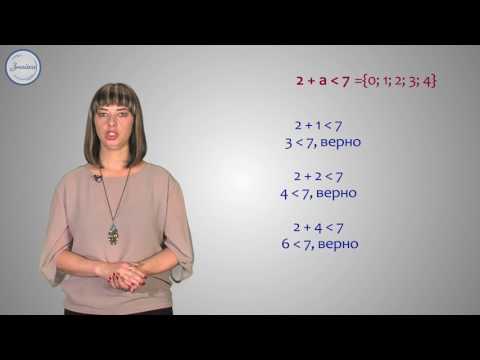 0:05:32
0:05:32
 0:06:41
0:06:41
 0:09:43
0:09:43
 0:08:55
0:08:55
 0:06:34
0:06:34
 0:10:46
0:10:46
 0:00:40
0:00:40
 0:10:52
0:10:52