filmov
tv
Related Rates #2 Using Cones
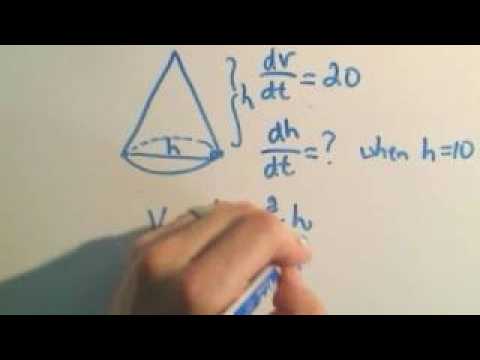
Показать описание
🪨 Master Related Rates with the Gravel Pile Problem! 🪨
In this informative calculus video, we explore a related rates problem involving a pile of gravel. As gravel is dumped into the pile, we’ll determine how quickly the height of the pile is changing. Understanding this concept is essential for applying related rates in real-world scenarios!
What You’ll Learn:
Understanding Related Rates: Grasp the fundamentals of related rates problems in calculus.
Step-by-Step Approach: Follow along as I guide you through the process:
Creating a Diagram: Visualize the gravel pile to clarify the relationship between variables.
Labeling Rates: Identify and label all relevant rates of change.
Finding the Equation: Establish the equation that relates the volume of the gravel pile to its height.
Taking the Derivative: Differentiate the equation with respect to time (d/dt) to relate the rates.
Substituting Values: Plug in specific information to solve for the rate at which the height is changing.
Why Watch This Video?
Ideal for Students: Perfect for high school and college students studying calculus and related rates.
Clear Explanations: Easy-to-follow instructions that simplify complex calculus concepts.
Enhance Your Problem-Solving Skills: Build confidence in tackling related rates problems in calculus.
📈 Don’t Forget to:
LIKE this video if you find it helpful!
SHARE with classmates or friends who want to master related rates!
SUBSCRIBE for more calculus tutorials, problem-solving techniques, and educational conten
#RelatedRates #Calculus #GravelPileProblem #MathTutorial #EducationalContent #LearningCalculus #ProblemSolving #HighSchoolMath #CollegeCalculus #DifferentialCalculus #MathConcepts #VisualLearning #RateOfChange #MathematicalProblemSolving
In this informative calculus video, we explore a related rates problem involving a pile of gravel. As gravel is dumped into the pile, we’ll determine how quickly the height of the pile is changing. Understanding this concept is essential for applying related rates in real-world scenarios!
What You’ll Learn:
Understanding Related Rates: Grasp the fundamentals of related rates problems in calculus.
Step-by-Step Approach: Follow along as I guide you through the process:
Creating a Diagram: Visualize the gravel pile to clarify the relationship between variables.
Labeling Rates: Identify and label all relevant rates of change.
Finding the Equation: Establish the equation that relates the volume of the gravel pile to its height.
Taking the Derivative: Differentiate the equation with respect to time (d/dt) to relate the rates.
Substituting Values: Plug in specific information to solve for the rate at which the height is changing.
Why Watch This Video?
Ideal for Students: Perfect for high school and college students studying calculus and related rates.
Clear Explanations: Easy-to-follow instructions that simplify complex calculus concepts.
Enhance Your Problem-Solving Skills: Build confidence in tackling related rates problems in calculus.
📈 Don’t Forget to:
LIKE this video if you find it helpful!
SHARE with classmates or friends who want to master related rates!
SUBSCRIBE for more calculus tutorials, problem-solving techniques, and educational conten
#RelatedRates #Calculus #GravelPileProblem #MathTutorial #EducationalContent #LearningCalculus #ProblemSolving #HighSchoolMath #CollegeCalculus #DifferentialCalculus #MathConcepts #VisualLearning #RateOfChange #MathematicalProblemSolving
Комментарии
 0:09:42
0:09:42
 0:08:38
0:08:38
 0:14:57
0:14:57
 0:10:46
0:10:46
 0:04:39
0:04:39
 0:05:31
0:05:31
 0:08:53
0:08:53
 0:07:22
0:07:22
 0:11:32
0:11:32
 0:04:45
0:04:45
 0:10:32
0:10:32
 0:01:00
0:01:00
 0:11:42
0:11:42
 0:13:31
0:13:31
 0:06:31
0:06:31
 0:03:49
0:03:49
 0:00:59
0:00:59
 0:19:36
0:19:36
 0:15:27
0:15:27
 0:03:51
0:03:51
 0:10:56
0:10:56
 0:07:20
0:07:20
 0:05:50
0:05:50