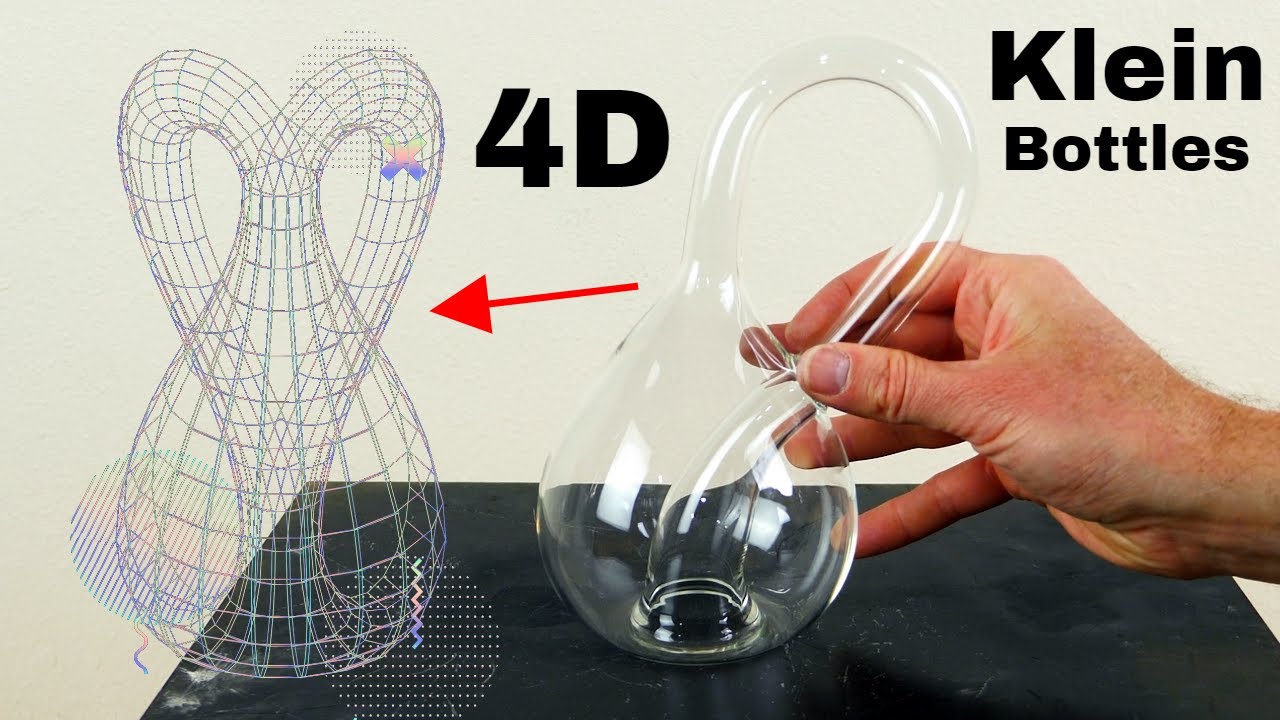
What Does a 4D Klein Bottle Look Like?

I show you what the difference is between a klein bottle in 4D vs 3D.

[TheActionLab]

Hello everyone, when I mentioned finding a higher price online than PCBway, obviously it was meant to mean if you find a lower price online they will match it! The point is they will give you a great price😁

[saidchammas]

I don't think i've ever seen someone explain a klein bottle and 4D so simply

[Square_Peg]

I just can't wrap my mind around what anything in the 4th dimension would look like

[Mad-vd]

Hey, The Action Lab. Actually a 2d person would not see a circle as you stated at 2:20, they would see a line. You, as an observer in the 3rd dimension would be able to see the entire circle that your finger imprints into the 2nd dimension, but a 2D person would not have the depth to see behind their vantage point to see the entire circle. Instead, they would be seeing a circle from the side, which to them would appear as a straight line.

[clintonleonard]

What terrifies me about this is that there could be 4D things all around us, permeating us, all the time, and we don't even know. They could look inside our bodies and inside of the most secure room on Earth. Like a 2d creature on a mobius strip would feel like it is walking on a flat plane, we are probably twisting and undulating in higher dimensions. It freaks me out.

[KateLB]

You are such an amazing teacher. I WISH that I had someone like you teaching my science classes in high school! I’m a scientist working in a laboratory now, but I can only imagine what else I would have been inspired to do with such great inspiration at an early age!

[kelvinle]

Another explanation is to have a portal on the "inside" and "outside" of the intersection. So instead of intersecting the surface, the Klein bottle will just go through that portal, thus completing the loop without intersecting itself.

[MuzikBike]

Finally some recognition for 4D Toys! An absolute masterpiece of a simulation program.

[fin]

these at 2am feels like im learning something

[exploshaun]

Since it's impossible for a 3D creature to see a 4D object I don't even bother trying to figure out what it looks like.

[tiusic]

I imagine 4D objects by mapping the 4th dimension to color. with the rule that if 2 things are different colors, they can pass through each other. Then you can imagine 4D klein bottle as a 3D one that's mostly red, but around where the intersection is it fades through orange to yellow. The yellow tube is able to pass through the red body without intersecting.

That sort of color change is the same as lifting up the crossing part of the figure 8 example.

[Rawny]

6:26 The "bottle", then the 2d line on paper then back to the "bottle" was a GREAT visual explanation! ty!

[cmyk]

Fun fact: the name “Klein bottle” was a misunderstanding. Its original name was “Klein surface” (Kleinsche Fläche), but since the German word looks similar to that for “bottle” (Flasche), and its 3D representation looks like a bottle, the mistaken name stuck.

[luckysnakerivals]

explaining everything unrelated and actually showing us the 4D Klein Bottle for 10 seconds

[kaysonhall]

Whenever I watch your videos, I have no idea what you’re talking about half the time, but that’s what makes it enjoyable.

[Bootleg_Jones]

You forgot to mention that in topology a beaker would be considered to have infinitely thin walls. A real like beaker definitely does have volume since it's walls do have thickness in real life.

[sophiedenise]

The "Dude... what if you... like... sewed two mobius loops together..." at 0:30 cracked me up

[hannesaltenfelder]

I've seen a video, that explains 0, 1, 2, 3...10d with shapes, that are somewhat pressed together, but instead of overlapping, that part is now in the next dimension.
Your video was the next puzzlepiece to kind of understanding a bit more.
Thank you very, very much.

[Quklasa]

I've always been fascinated by non-orientable shapes, this was such an interesting way to help someone understand it!

[hyperion]

My brain dies everytime I try to comprehend the 4th dimension