filmov
tv
Geometry 7.2a, Dilations & Similarity Transformations

Показать описание
An explanation of a dilation as a transformation that maps (x,y) to (kx, ky) where k is greater than 0, has a center at (0,0), and scale factor k. How similarity ratios are scale factors, drawing and describing dilations, how the pre-image and image of dilations are similar, similarity transformations, and finally determining whether polygons are similar.
High School Geometry Playlist
FOLLOW ME:
SUPPORT MY WORK:
Get a JoAnn's School t-shirt, mug, tote, hoodie,
or inspirational sticker to let everyone know you're a fan!
High School Geometry Playlist
FOLLOW ME:
SUPPORT MY WORK:
Get a JoAnn's School t-shirt, mug, tote, hoodie,
or inspirational sticker to let everyone know you're a fan!
Geometry 7.2a, Dilations & Similarity Transformations
Geometry 7-2: Similarity Transformation
Math 2 - Module 6.2 Dilation and Similarity Part 1
Geometry 7.6a, Dilations & Similarity in the Coordinate plane
Testing similarity through transformations | Similarity | Geometry | Khan Academy
Similar Triangles | MathHelp.com
Similar Triangles
N-Gen Math Geometry.Unit 7.Lesson 5.Similarity Criteria
Similar Triangles and Figures, Enlargement Ratios & Proportions Geometry Word Problems
Dilation Transformations | Scale Factors | Geometry | Eat Pi
Geomtry Lesson 9.7 Similarity Transformations
N-Gen Math Geometry.Unit 7.Lesson 1.Dilations
Unit 6 Similarity - Compositions of Transformations with Dilations
GeoTrig - Week 15 - 9-6 & 9-7 Dilations and Similarity
Geometry 7.2b, Proving Circles Similar
Geometry QL4 dilation to similarity
Dilations: Why Do They Make Sense? (Positive Scale) Easy and Fast Explanation
Math 8.2.2 Dilations & Similarity
Geometry - Ch. 12.7: Dilations (pt. 1 of 2)
Geometry Notes T.7 Dilations
Geometry 9.6: Dilations
8th TAP, section 7.6 - Dilation and Similarity
Math II 8.1 Dilations Part One
Unit 5: Similarity Lesson 2: Dilations
Комментарии
 0:08:57
0:08:57
 0:13:21
0:13:21
 0:03:45
0:03:45
 0:12:04
0:12:04
 0:02:11
0:02:11
 0:01:40
0:01:40
 0:11:40
0:11:40
 0:27:58
0:27:58
 0:18:04
0:18:04
 0:13:46
0:13:46
 0:04:47
0:04:47
 0:30:02
0:30:02
 0:59:51
0:59:51
 0:04:57
0:04:57
 0:05:58
0:05:58
 0:13:34
0:13:34
 0:07:02
0:07:02
 0:18:18
0:18:18
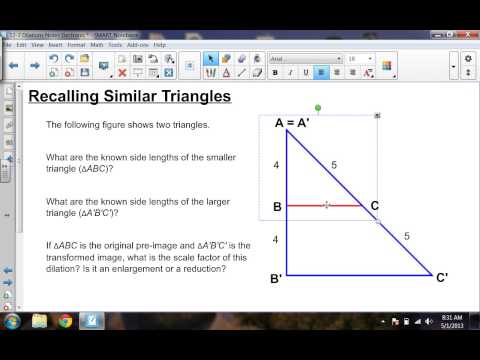 0:10:03
0:10:03
 0:17:41
0:17:41
 0:08:09
0:08:09
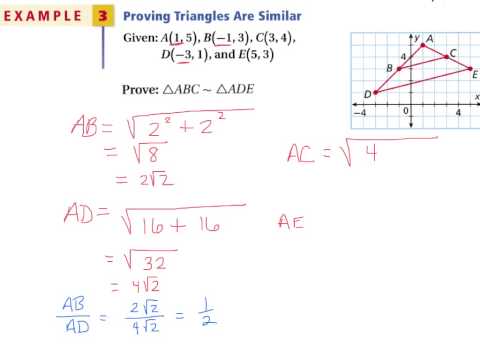 0:07:46
0:07:46
 0:07:36
0:07:36
 0:05:26
0:05:26