Limit of sin(x^2 + y^2)/(x^2 + y^2) using Polar Coordinates and L'Hopital's Rule

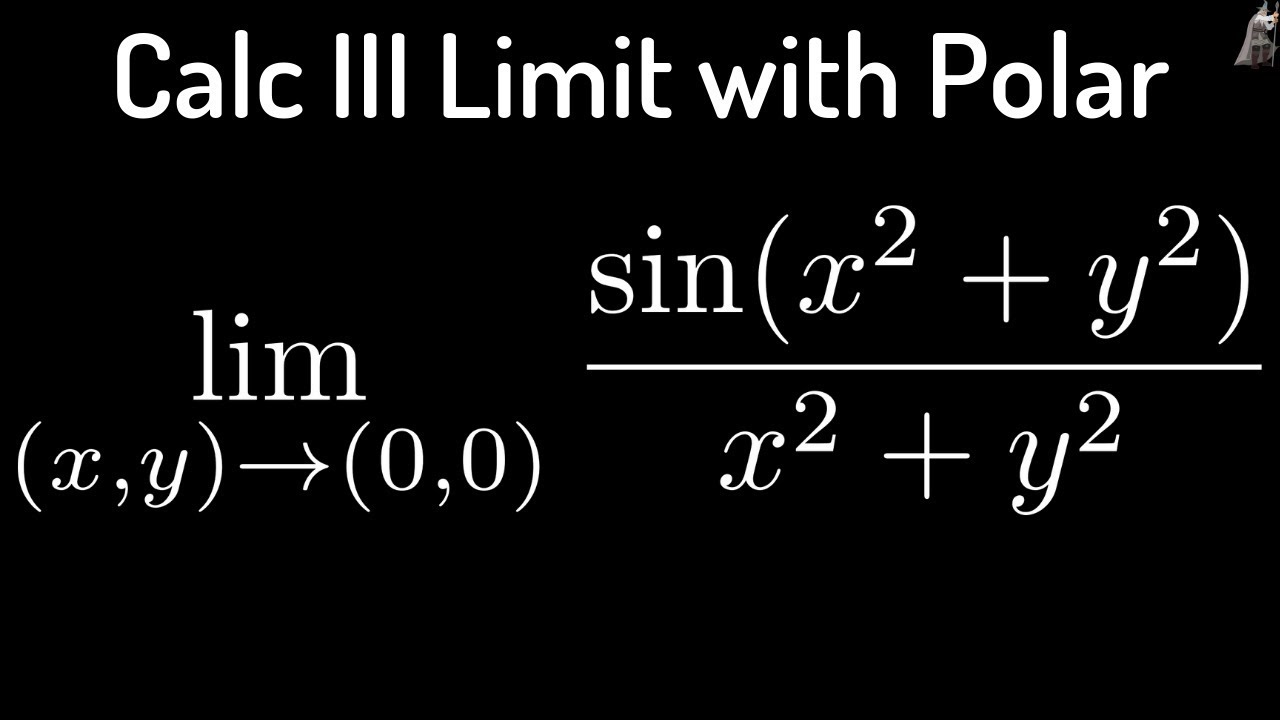
preview_player
Показать описание
Limit of sin(x^2 + y^2)/(x^2 + y^2) using Polar Coordinates and L'Hopital's Rule
  1. The Math Sorcerer
  2. L'Hôpital's Rule
  3. Limit
  4. Polar Coordinate System
  5. Sine
  6. Calculus (Field Of Study)
Рекомендации по теме
Limit of sin(x^2 0:01:54

Limit of sin(x^2 + y^2)/(x^2 + y^2) using Polar Coordinates and L'Hopital's Rule

lim (x,y) approaches 0:01:05

lim (x,y) approaches (0,0) of sin(x^2+y^2)/(x^2+y^2)

Multivariable Calculus Limit 0:03:53

Multivariable Calculus Limit of x^2y/(x^2 + y^2) using Polar Coordinates

the value of 0:01:49

the value of `lim_(x- gty) (sin^2x-sin^2y)/(x^2-y^2)` equals

Multivariable Calculus Limit 0:03:06

Multivariable Calculus Limit of y^2/(x^2 + y^2) as (x,y) approaches (0,0)

#Trigonometry all formulas 0:00:16

#Trigonometry all formulas

Limits of multivariable 0:11:35

Limits of multivariable functions

Continuity and Differentiability 2:55:04

Continuity and Differentiability 12 | Part 1 | One Shot in English | JEE Main & Advanced

Limit Trigonometric Function 0:08:13

Limit Trigonometric Function (1 - cos2x)/x^2 Half angle Formula application

How REAL Men 0:00:35

How REAL Men Integrate Functions

Area bounded by: 0:11:52

Area bounded by: y=x^2+2, y=sin⁡(x), x=-1, x=2 | Area under the curve | Application of Integration...

Find derivative implicitly 0:04:19

Find derivative implicitly to find equation tangent line at (0, 1/2) x^2 + y^2 = (2x^2 + 2y^2 -x)^2

When mathematicians get 0:00:37

When mathematicians get bored (ep1)

🟡05 - Limit 0:26:31

🟡05 - Limit and Continuity of Functions of Two Variables

sin(x^2 * y^2) 0:02:15

sin(x^2 * y^2) = x find dy/dx using implicit differentiation

lim (x,y) approaches 0:00:37

lim (x,y) approaches (0,0) of e^y sinx/x

Find derivative implicitly 0:05:45

Find derivative implicitly with respect to x for y sin (x^2) = x sin (y^2)

Limit x^2(3 + 0:03:26

Limit x^2(3 + sin(x))/(x + sin(x))^2 as x approaches zero Calculus 1 Limits with sinx/x

IIT Bombay CSE 0:00:11

IIT Bombay CSE 😍 #shorts #iit #iitbombay

5 simple unsolvable 0:00:50

5 simple unsolvable equations

Memorization Trick for 0:00:15

Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school

when calculus students 0:00:43

when calculus students use trig identities too early

f(x,y)= (x2-y2) /(x2+y2) 0:08:39

f(x,y)= (x2-y2) /(x2+y2) Show that the repeated limit exist and are unequal but the double limit .

lim [sin(x)(1-cosx))/x^2, trig 0:01:01

lim [sin(x)(1-cosx))/x^2, trig limit example(watch to end to see all work in one place)

Комментарии
Автор

So the trick was that r^2=x^2+y^2... Great and efficient explanation! Thanks

alexcodema
Автор

So efficient! learning us this in under 2 minutes!

YB
Автор

Can you calculate this limit without polar coordinates?

degenerationz
Автор

On break and still going' ham.. Good man!

vedgsesh
Автор

What happen if x and y are too general that can’t map to the polar coordinates?

ToanLe-njiu
Автор

Hey . How should i approach limit of when x goes to 0 and y goes to 0

notAlexanderOFF
Автор

if I have this case: lim (x, y)->(1, 1) sin(x^2-y^2)/(x-y) what is the correct procedure in order to obtain 2??

nachoman
Автор

My problem is similar is Limit sen(x^2+y^2+z^2)/x^2+y^2+z^2 in (x, y, z) a 0

fernandolopez-dzui
Автор

How to evaluate lim (x, y) tends to (0, 0) xsin(x^2+y^2)/(x^2+y^2) ? Please help...

bhaskardas