filmov
tv
Calculus 1: How to use the intermediate value theorem
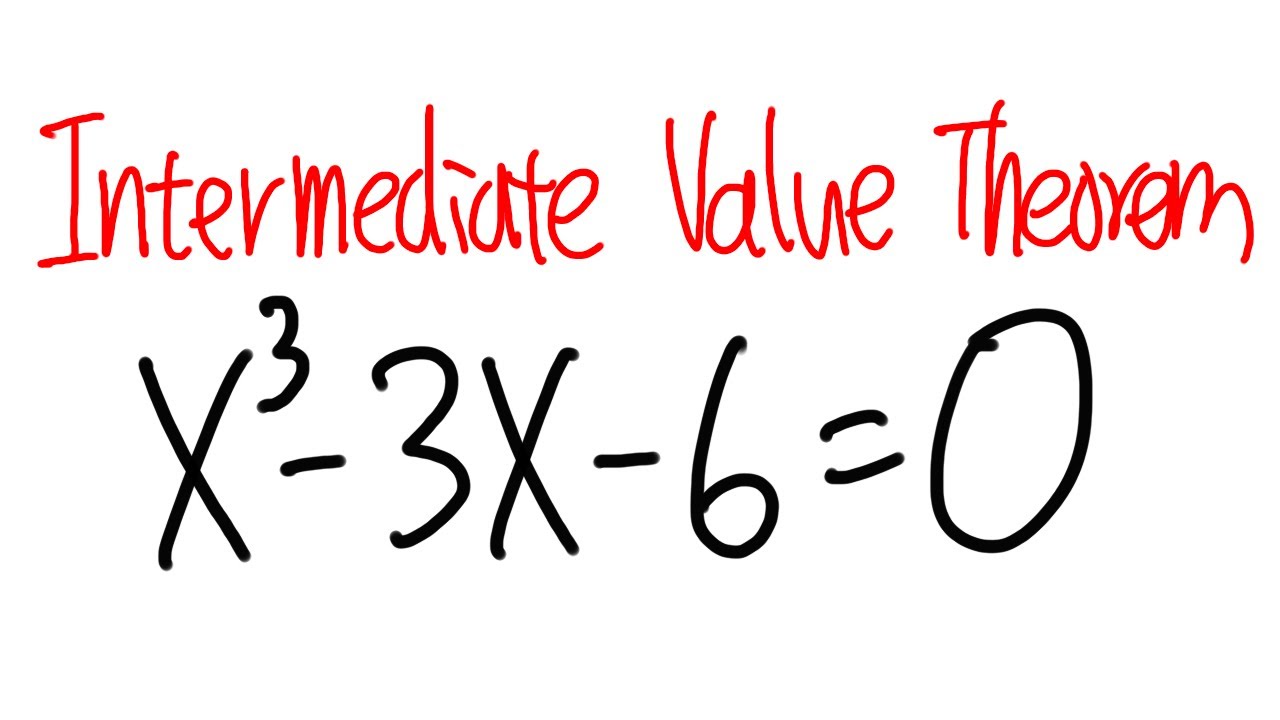
Показать описание
Here's an example of how we can use the intermediate value theorem. The cubic equation x^3-3x-6=0 is quite hard to solve but we can use IVT to determine where the solution has to be. Remember the IVT is for continuous functions only. It is useful when we have to determine an interval that has a root to a continuous function.
Use "WELCOME10" for 10% off
---------------------------------------------------------
😊 Thanks to all calculus supporters 😊
Sandglass Dªrksun Seth Morris Andrea Mele
-----------------------------
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math
Use "WELCOME10" for 10% off
---------------------------------------------------------
😊 Thanks to all calculus supporters 😊
Sandglass Dªrksun Seth Morris Andrea Mele
-----------------------------
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math
Understand Calculus in 35 Minutes
Calculus in a nutshell
Understand Calculus in 10 Minutes
Calculus 1 - Derivatives
What is Calculus used for? | How to use calculus in real life
Introduction to Calculus (1 of 2: Seeing the big picture)
Calculus 1 - Introduction to Limits
The essence of calculus
How to use squeeze theorem to show that a limit = 0 (Calculus 1 2.3 WebAssign)
Understand Calculus in 1 minute
HOW TO USE CALCULUS IN THE REAL WORLD?
Calculus made EASY! 5 Concepts you MUST KNOW before taking calculus!
Calculus, what is it good for?
Why is calculus so ... EASY ?
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
calculus 1 tutorial: how to use the product rule, quotient rule, and chain rule
Calculus 1 - Full College Course
Become a Calculus Master in 60 Minutes a Day
Calculus 1 - Integration & Antiderivatives
Calculus 1 Final Exam Review
Introductory Calculus: Oxford Mathematics 1st Year Student Lecture
Introduction to integral calculus | Accumulation and Riemann sums | AP Calculus AB | Khan Academy
Integration (Calculus)
Derivative as a concept | Derivatives introduction | AP Calculus AB | Khan Academy
Комментарии
 0:36:22
0:36:22
 0:03:01
0:03:01
 0:21:58
0:21:58
 0:52:51
0:52:51
 0:11:39
0:11:39
 0:12:11
0:12:11
 0:20:20
0:20:20
 0:17:05
0:17:05
 0:02:58
0:02:58
 0:00:57
0:00:57
 0:07:07
0:07:07
 0:23:44
0:23:44
 0:07:43
0:07:43
 0:38:32
0:38:32
 0:20:46
0:20:46
 0:11:44
0:11:44
 11:53:48
11:53:48
 0:09:49
0:09:49
 0:40:04
0:40:04
 0:55:58
0:55:58
 0:58:03
0:58:03
 0:04:52
0:04:52
 0:07:04
0:07:04
 0:07:16
0:07:16