filmov
tv
Solving the Exponential Equation 2^(3x - 2) + 8^(x - 1) = 0

Показать описание
Solving the Exponential Equation 2^(3x - 2) + 8^(x - 1) = 0
(these are my affiliate links)
***********Math, Physics, and Computer Science Books***********
These are my affiliate links. As an Amazon Associate I earn from qualifying purchases.
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
(these are my affiliate links)
***********Math, Physics, and Computer Science Books***********
These are my affiliate links. As an Amazon Associate I earn from qualifying purchases.
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
Solving the Exponential Equation 2^(3x - 2) + 8^(x - 1) = 0
Solving the Exponential Equation (1/2)^(3x - 6) = 8^(x + 1)
Can you solve this exponential equation? |2^x + 2^(3x) = 10
Exponential Equation | 2^(3x+1) - 3(2^2x) + 2^(x+1) = 2^x
Solve the Exponential Equation 2^2x+3 + 1 = 9x2^x
Exponential Equations Problem Solving : 3^(2-3x) = 4^(2x+1)
Solving (x^2-3x+1)^{x+1}=1 | An Exponential Equation
Exponential Equation: Solve 9^{x-3} = 27^{2x}
SAT Math on Khan Academy: Algebra (Medium)
Exponential Equation| Unique Exponential | Absolute Value | Solve x=–x^(x^2–3x+4/2x) for x
Solve for x natural exponential equation, e^(x^2) = e^(3x) times 1/e^2, (e^4)^x times e^(x^2) = e^12
An Exponential Equation | 2^{x+3}=3^{x+2}
A Nice Math Olympiad Exponential Equation 3^x = X^9
Solving the Exponential Equation e^(3x - 1) = (e^x)^2
Solving Exponential Equation
Solving Exponential Equations
Can you solve this? | Exponential Equation | Algebra Problem.
How to Solve 2^(x - 2) = 3^(2x - 4) Exponential Equation with Different Base with Logarithms
Solve the Exponential Equation 2^(3x)*5^(3x+1)=7^(-2x) - Step-by Step Explanation.
Exponential Equation | Finding Real Solution | Solve 2^x + 2^3x = 10 for X | Math Olympiad Question
Exponential Equation | 2²ˣ⁺¹-9(2ˣ)+4=0
😳 CLEAN BASIC MATHEMATICS 2^3x+1/2=1/16 Exponential Equation NO ONE CAN SOLVE1 #Shorts
Solve an exponential equation by taking log of both sides & approximating the value
Learn how to solve an exponential equation 2^(x-3) = 32
Комментарии
 0:03:39
0:03:39
 0:02:24
0:02:24
 0:04:33
0:04:33
 0:04:44
0:04:44
 0:07:24
0:07:24
 0:03:10
0:03:10
 0:05:08
0:05:08
 0:01:04
0:01:04
 0:46:21
0:46:21
 0:10:20
0:10:20
 0:03:11
0:03:11
 0:00:52
0:00:52
 0:02:34
0:02:34
 0:00:55
0:00:55
 0:00:56
0:00:56
 0:16:36
0:16:36
 0:03:33
0:03:33
 0:05:06
0:05:06
 0:05:43
0:05:43
 0:04:08
0:04:08
 0:03:39
0:03:39
 0:00:13
0:00:13
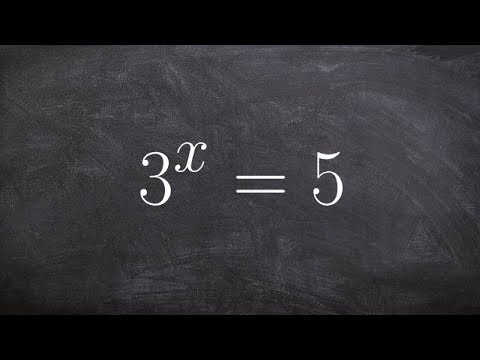 0:03:23
0:03:23
 0:01:39
0:01:39