Calculus 3: Triple Integrals (8 of 25) Volume of a Rotated Curve: Method 1: Cylindrical

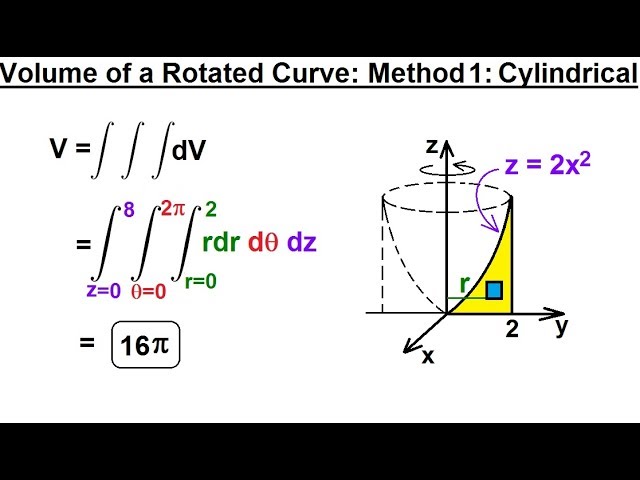
In this video I will find volume of a rotated curve z=2x^2 using triple integrals in the cylindrical coordinate system.

Next video in this series can be seen at:

[stevedasilvaferreira]

Less confusing, if add lower limit of integration as x=root(z/2) or alt, use integral limits for z from 0 to 2, we will get twice Volume, which means that necessary to half sphere, or alt, take half the limit of integration for 2pi--->>π for half circle, with limits in z 0 to 2

[rafakordaczek]

There is a mistake - paraboloid have a formula z=x^2+y^2 instead of z=2x^2. Therefore z=2x^2 is not a rotated curve. The equation says that no matter what you will choose, you will have the same parabola.

[MohamedEllebody--]

can you explain in another way why the r limits from x to 2

[jaddoumit]

I don't get it . why does r go from x to 2 instead of 0 to 2?

There is no need for rdrdθdz. Much easier and less confusion with rdzdrdθ.