filmov
tv
Unbiased Estimators (Why n-1 ???) : Data Science Basics

Показать описание
Finally answering why we divide by n-1 in the sample variance!
Unbiased Estimators (Why n-1 ???) : Data Science Basics
What is an unbiased estimator? Proof sample mean is unbiased and why we divide by n-1 for sample var
Proof that the Sample Variance is an Unbiased Estimator of the Population Variance
Review and intuition why we divide by n-1 for the unbiased sample | Khan Academy
The Sample Variance: Why Divide by n-1?
Why Sample Variance is Divided by n-1
Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance
Variance: Why n-1? Intuitive explanation of concept and proof (Bessel‘s correction)
Unbiasedness vs consistency of estimators - an example
Why We Divide by N-1 in the Sample Variance (The Bessel's Correction)
An unbiased estimator of the population variance
Biased and unbiased estimators from sampling distributions examples
Unbiased estimator : Sample variance, Why divide by n-1 - very intuitive
3.2.2 Measures of Variation - Introduction to Biased and Unbiased Estimators
How to tell if an estimator is biased or unbiased
Simulation providing evidence that (n-1) gives us unbiased estimate | Khan Academy
(IS05) Unbiased Estimators
Estimation Theory | Unbiased estimator | L17
Proof ols estimator is unbiased
Unbiased Estimator for the Variance | Full Derivation
Unbiased Estimation
Unbiased Estimator
Unbiased Estimator of Variance (to divide by n or n - 1)
The Sample Mean is a Consistent Estimator of the Population Mean
Комментарии
 0:08:35
0:08:35
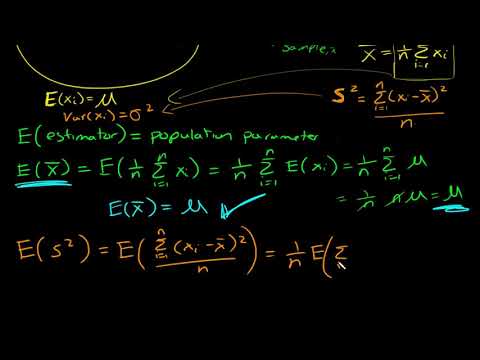 0:17:12
0:17:12
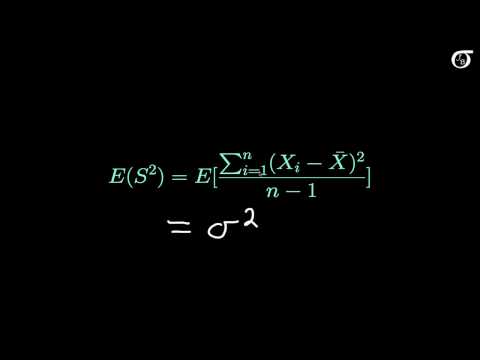 0:06:58
0:06:58
 0:09:44
0:09:44
 0:06:53
0:06:53
 0:09:03
0:09:03
 0:04:46
0:04:46
 0:30:13
0:30:13
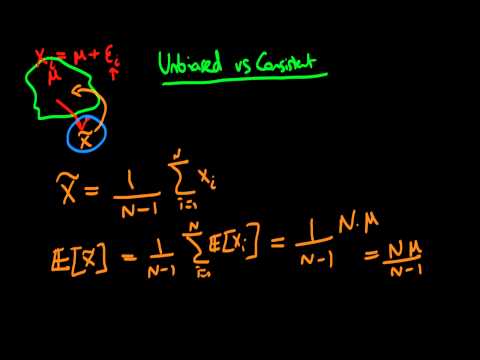 0:04:09
0:04:09
 0:06:21
0:06:21
 0:06:05
0:06:05
 0:05:56
0:05:56
 0:11:25
0:11:25
 0:13:51
0:13:51
 0:01:41
0:01:41
 0:04:30
0:04:30
 0:32:14
0:32:14
 0:49:51
0:49:51
 0:14:38
0:14:38
 0:32:59
0:32:59
 0:20:27
0:20:27
 0:04:57
0:04:57
 0:14:13
0:14:13
 0:03:37
0:03:37