filmov
tv
Find a + b = ? if a^3 + b^3 - 3ab =1 | Olympiad Question

Показать описание
We rewrite the given condition in terms of a + b using the (a + b)^3 formula. Then use the product of all roots formulas to find the first solution for a + b. Then we use the completing the square method to find the second solution for a + b.
AB and BA matrix multiplication solving simple way
Find the values a and b that make the piecewise function continuous
Letter Game | Find the Letter B | The Singing Walrus
SHORTCUT - HOW TO FIND A AND B THAT MAKE PIECEWISE FUNCTION CONTINUOUS EVERYWHERE
Can you find the value of angle sum? | (a+b+c+d+e+f) | #math #maths | #geometry
Find a+b+c+d
Find a and b if f(x) is continuous everywhere
Find A-B and B-A if A={1,2,3,4,5} and B={4,5,6,7} are they equal?
Solve (√3+1)/(√3-1)=a+b√3 . Find a and b
I Built a SECRET Pool in My Room!
Find the values a and b that make the function differentiable
Find ab, if a+b= 7, and a-b= 4.
Find Matrix A & B If matrix A+B & A-B given|Matrices|ALJEBRA|Maths|Aptitude|12th|Diploma|B.T...
46. Find the values of a and b that make f continuous everywhere. F(x)={(x^2-4)/(x-2) if x⋖2,
If a+b=9 and ab=20 then find the value of a²+b²? || Algebraic Identities || (a+b)²=a²+2ab+b²
Find the distance between the following pairs of points: (iii)(a,b),(-a,-b)
Don Q & B Lovee - Come Find Us [Official Video]
Ex: Find sin(a+b) and cos(a-b) given sin(a) and cos(b)
Find the Values of a and b Such That the Piecewise Function is Differentiable Everywhere (Calculus)
How to Find a and b so that the Piecewise Function is Continuous Everywhere
Given matrix A and matrix B. Find (if possible) the matrices: (a) AB (b) BA ... | Plainmath
If a2+b2=41 and ab = 20 find a+b a-b a and b
Baby B - Find You ( Official Audio)
If a+b=3 and ab=2 then find the value of a^3+b^3.
Комментарии
 0:03:28
0:03:28
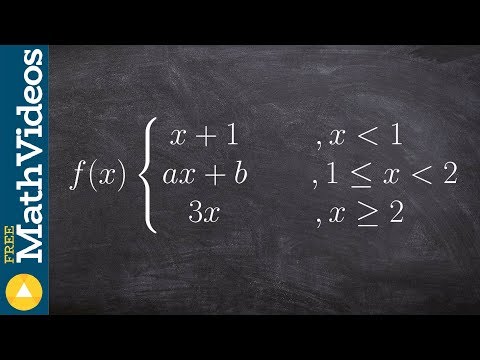 0:03:44
0:03:44
 0:02:28
0:02:28
 0:06:27
0:06:27
 0:04:56
0:04:56
 0:11:13
0:11:13
 0:10:36
0:10:36
 0:01:59
0:01:59
 0:03:11
0:03:11
 0:26:27
0:26:27
 0:06:05
0:06:05
 0:01:14
0:01:14
 0:10:02
0:10:02
 0:06:37
0:06:37
 0:01:29
0:01:29
 0:01:40
0:01:40
 0:03:10
0:03:10
 0:06:41
0:06:41
 0:04:01
0:04:01
 0:10:48
0:10:48
 0:05:07
0:05:07
 0:03:21
0:03:21
 0:03:12
0:03:12
 0:02:49
0:02:49