filmov
tv
An Infinite Sum from the Berkeley Math Tournament

Показать описание
What's this infinite sum?
A visual infinite sum like you’ve never seen!
Finite sum of an infinite series
An Infinite Sum from the Berkeley Math Tournament
A Classic Infinite Series - Made Simple
Sum of an infinite geometric series | Sequences, series and induction | Precalculus | Khan Academy
sum of finite series/nth sum of infinite series #shorts #youtubeshorts
How to use the Integral Test to Approximate an Infinite Sum
Finding The Sum of an Infinite Geometric Series
sum of an infinite geometric series
Sum of an Infinite Geometric Series, Ex 3
Sum of an Infinite Geometric Series | Math Video Central
Two Nonstandard Infinite Geometric Series (visual proof)
Infinite Series Formulas
Infinite sum of powers of sixths!
Infinite Series - Numberphile
Finding an infinite sum with triangles!
Sum of the Infinite Series: SUM(e^(npi)/n!) #shorts
Infinite sum of powers of 4/9
Infinite Sums | Geometric Series | Explained Visually
Ex 2: Find the Sum of an Infinite Geometric Series
Infinite series Defining the sum of an infinite series
Summing An Infinite Geometric Series
Infinite Geometric Series Sum
Комментарии
 0:00:31
0:00:31
 0:00:57
0:00:57
 0:04:54
0:04:54
 0:24:15
0:24:15
 0:01:00
0:01:00
 0:04:46
0:04:46
 0:00:16
0:00:16
 0:03:32
0:03:32
 0:19:50
0:19:50
 0:00:11
0:00:11
 0:03:40
0:03:40
 0:05:33
0:05:33
 0:03:21
0:03:21
 0:00:05
0:00:05
 0:00:55
0:00:55
 0:09:31
0:09:31
 0:01:00
0:01:00
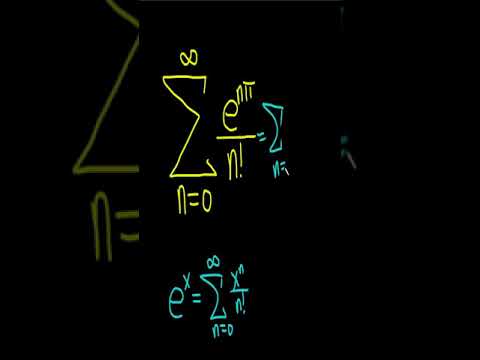 0:00:39
0:00:39
 0:00:52
0:00:52
 0:02:47
0:02:47
 0:03:59
0:03:59
 0:05:32
0:05:32
 0:00:43
0:00:43
 0:00:45
0:00:45