filmov
tv
10 - What are Imaginary Numbers?
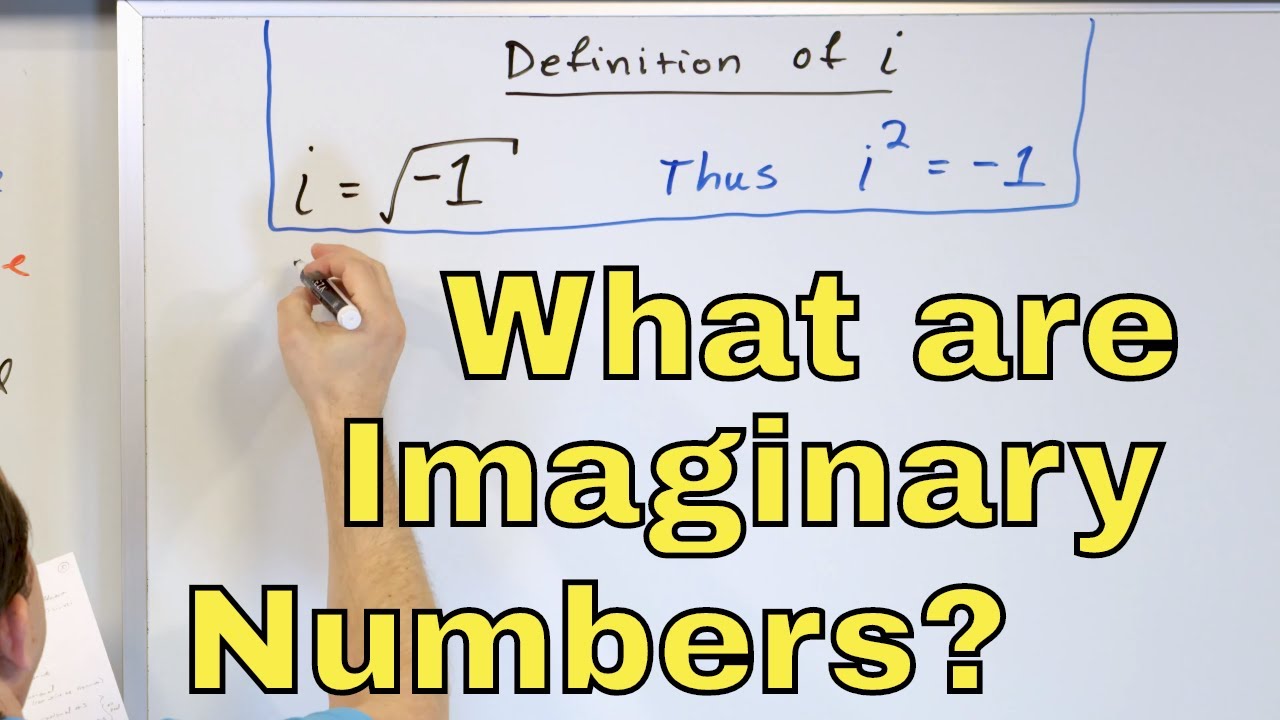
Показать описание
In this lesson, we will explore the concept of the imaginary number in algebra. We will discuss that for each new type of equation in algebra, a new type of number was needed to solve the equation. For equations involving square roots, we need the concept of the imaginary number "i", which is the square root of negative 1. In parallel with this, we know that i^2 is equal to -1. We explore how to take the square root of negative numbers using imaginary numbers and discuss their significance.
10 - What are Imaginary Numbers?
Imaginary Numbers Are Real [Part 10: Complex Functions]
How Imaginary Numbers Were Invented
Imaginary Numbers - Basic Introduction
Where do Imaginary Numbers come from?
Imaginary Numbers Are Real [Part 1: Introduction]
Complex Numbers - Introduction to Imaginary Numbers | Don't Memorise
What are the Types of Numbers? Real vs. Imaginary, Rational vs. Irrational
What's the physical meaning of imaginary numbers?
Introduction to complex numbers | Imaginary and complex numbers | Precalculus | Khan Academy
Are Imaginary Numbers Real?
Imaginary Numbers || Basic Concept
iMaGiNaRy nUmBeRs
Life of Luxury - Tommy and imaginary friend But with Healthbars
Simplifying imaginary numbers to higher exponents
Top 10 Imaginary Friends That Were Actually Ghosts
Top 10 Imaginary Authors Fragrances | Brand Overview
Modeling Engineered Systems Lecture 10: Imaginary Numbers Continued
ACT Math - Ultimate Guide to Complex and Imaginary Numbers
Top 10 Signs Your Child's Imaginary Friend Is Actually A Ghost
Top 10 Demons Pretending To Be Imaginary Friends
Imaginary (2024) Official Trailer – DeWanda Wise, Tom Payne, Taegen Burns
Top 10 Imaginary Friends Who Haunted Children
Bing Bong in Inside Out 2?! #disney #pixar #easteregg #animation #imaginary
Комментарии
 0:38:00
0:38:00
 0:07:29
0:07:29
 0:23:29
0:23:29
 0:14:12
0:14:12
 0:01:00
0:01:00
 0:05:47
0:05:47
 0:04:50
0:04:50
 0:09:00
0:09:00
 0:06:03
0:06:03
 0:04:44
0:04:44
 0:05:54
0:05:54
 0:03:18
0:03:18
 0:00:10
0:00:10
 0:00:19
0:00:19
 0:06:08
0:06:08
 0:10:39
0:10:39
 0:18:45
0:18:45
 0:08:20
0:08:20
 0:14:20
0:14:20
 0:10:55
0:10:55
 0:10:50
0:10:50
 0:02:31
0:02:31
 0:10:01
0:10:01
 0:00:53
0:00:53