Bead chain fountain - the Mould effect - Slow mo of computer sim

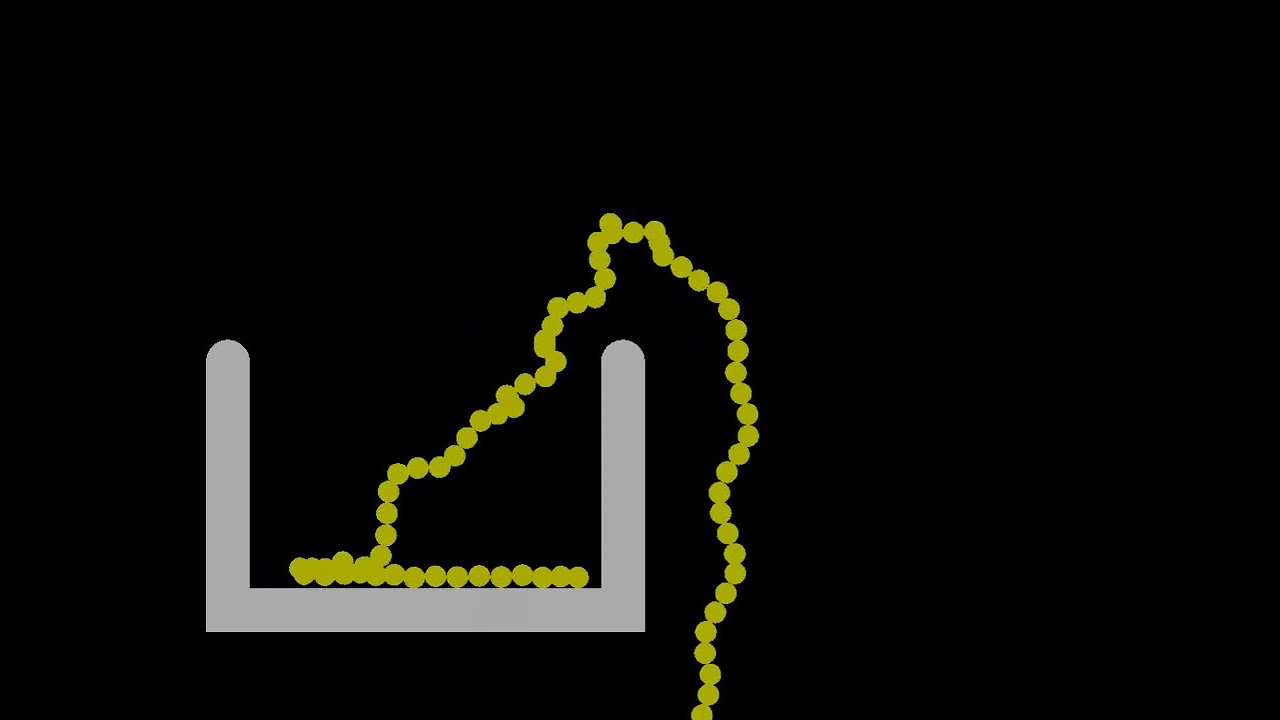
This slow motion recording of a dynamic simulation/analysis (FEA - Finite Element Analysis) explains the mould-effect (bead siphon, chain fountain) and is showing the initial behaviour ("first split second") before the bead chain siphon has stabilized properly. It shows that the siphon's driving force may at least be explained by two effects: 1. Inertia effects (i.e. Newton's first law of motion) and 2. Contact impact (kickback force) and possibly chain stiffness (this simulated chain has no stiffness from one bead to another, see description of boundary conditions below). The kickback force between the beads and the bottom of the container can be seen in this video if you look carefully; the beads tendency to "dance" up and down somewhat is evident and also check of the reaction force in the simulation between the beads and the bottom verifies this.

As the bead chain inside the container are lifted upwards due to the falling bead chain outside the container, initially the chain follows the container upper edge. However, as falling speed outside the container increases, due to inertia the upmoving beads get harder and harder to turn downwards. Hence the siphon height will increase with increasing speed. This is exactly what this computer simulation shows. Also the kickback force increases as the speed increases, and therefore contributes in the increasing height as well.

Also, lift may be generated due to under-pressure at the outside of the arc, as demonstrated by another video on my channel.

The FE Model is built with the following boundary conditions:

-Standard gravity
-Initial speed and speed ramped up continuosly
-contact defined between container bottom and beads and walls and beads
-each bead connected to its neighbour by the two coincident nodes merged together, i.e. beads freely rotates relative to each other, i.e. no connection stiffness

[physforfun]

Anyone know "status" the bet between Steve and Mehdi? Know it's just an unformal and friendly bet just for fun - but still would be interesting to know the standing as per now and when it's supposed to be settled with a final "winner"🤓

[MiguelGarcia-zxqj]

Thanks for your reply to my comment to the SM vídeo. And, yes, this simulations seems more to the point about what really happens in the bead fountain :)

[lioelbammalf]

Can you run this with a connecting band between the beads and run it, for comparison, with different length bands between the beads to see how it effects the height of the fountain?

[MaoriGo-tx]

Hi do you confirm that the chain reaches a constant speed at some point?

[andersmusikka]

Cool! Does the model transfer any torque between beads, or is it just point masses with forces between them?