filmov
tv
Integral of (ln(cos x))^3

Показать описание
Finishing our epic saga, we present the integral of (ln(cos x))^3 over the interval 0 to pi/2.
Integral of (ln(cos x))^3
Integral of ln(cos x)
Integral 11tan(x)ln(cos(x))
ln(cos x) integrals -- Teaser Trailer
Integration of ln x^3 (Solution)
Calculus Made Easy: Derivative of ln(cos(x)) Using the Chain Rule
Integral of ln(cos x) | Easier Way | step by step Tutorial | Important Calculus skills
Integration of ln(cosx) from 0 to pi/2
Integral of lnx
Integration by Parts the Integral of cos(ln(x))
find the integral of tan x ln(cos x)dx
6.14s Selecting Integration Techniques, ln(3x^2+1) - Calculus
HOW TO DIFFERENTIATE ln(cos(x))??? (COSINE FUNCTION, NATURAL LOGARITHM FUNCTION, CHAIN RULE, LOGS)
integral of cos(ln(x)), integration by parts (w/ u-sub vs without u-sub)
Integral of (ln(cos x))^2
How REAL Men Integrate Functions
when calculus students use trig identities too early
Integral 2 tanx ln(cosx)
Integral of ln(x) fast!
integral of e^(ln cos x) sec x dx
A crazy complex integral! - feat. Milo [ ln(cos(x))ln(sin(x))/tan(x) from 0 to pi/2 ]
Why ∫ln(cos(x)) dx [0, π/2] = ∫ln(sin(x)) dx [0, π/2] = -ln(2)π/2 ??
Derivative of ln[ln(cos x)], chain rule practice
indefinite integral ln(cos(x)^sin(x)) by substitution and parts | by parts | silent integrals
Комментарии
 0:29:47
0:29:47
 0:13:58
0:13:58
 0:03:33
0:03:33
 0:00:58
0:00:58
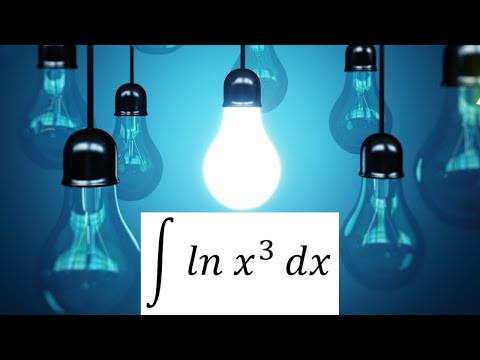 0:02:30
0:02:30
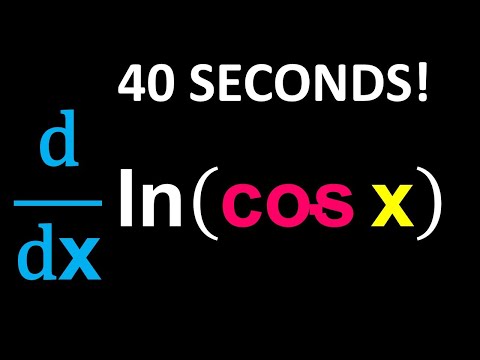 0:00:42
0:00:42
 0:11:52
0:11:52
 0:09:05
0:09:05
 0:01:26
0:01:26
 0:05:48
0:05:48
 0:01:12
0:01:12
 0:01:00
0:01:00
 0:08:32
0:08:32
 0:14:56
0:14:56
 0:25:45
0:25:45
 0:00:35
0:00:35
 0:00:43
0:00:43
 0:01:04
0:01:04
 0:00:45
0:00:45
 0:01:01
0:01:01
 0:09:34
0:09:34
 0:05:02
0:05:02
 0:00:55
0:00:55
 0:02:44
0:02:44