filmov
tv
Prim's Algorithm - Minimum Spanning Tree - Min Cost to Connect all Points - Leetcode 1584 - Python

Показать описание
0:00 - Read the problem
3:44 - Drawing Explanation
16:32 - Coding Explanation
leetcode 1584
#prims #algorithm #python
Disclosure: Some of the links above may be affiliate links, from which I may earn a small commission.
3.5 Prims and Kruskals Algorithms - Greedy Method
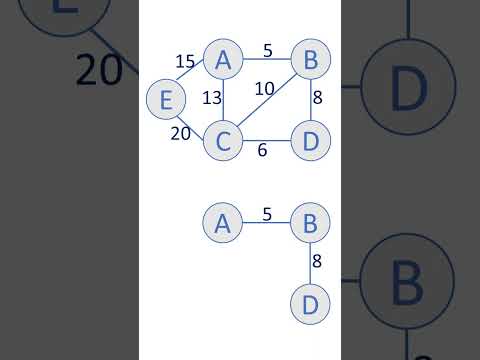
Prim's Algorithm
Prim's Algorithm - Minimum Spanning Tree - Min Cost to Connect all Points - Leetcode 1584 - Pyt...
L-4.9: Prim's Algorithm for Minimum Cost Spanning Tree | Prims vs Kruskal
Prim's Minimum Spanning Tree Algorithm | Graph Theory
G-45. Prim's Algorithm - Minimum Spanning Tree - C++ and Java
Prim's algorithm | Minimum Spanning tree (MST) | Design & Algorithms | Lec-26 | Bhanu Priya
Proof of Prim's MST algorithm using cut property
PRIM'S ALGORITHM (MINIMUM SPANNING TREE) || GRAPH
Prim's Algorithm: Minimal Spanning Tree
Minimum spanning tree || prims algorithm in data structure || 63 ||Data structures in telugu
Prim's Algorithm | Minimum Spanning Tree | Full Dry Run | INTUITION | Graph Concepts & Qns ...
12. Greedy Algorithms: Minimum Spanning Tree
Networks: Prim's Algorithm for finding Minimum spanning trees
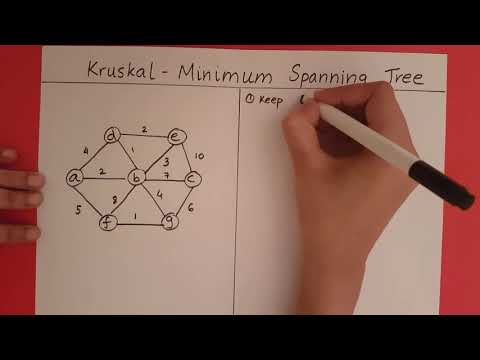
Kruskal's Algorithm
Prim's Algorithm for Minimum Cost Spanning Tree
Prim's Algorithm for minimum spanning trees || GATECSE || DAA
Prim's Algorithm for Minimum Spanning Trees (MST) | Graph Theory
OCR MEI MwA E: Minimum Spanning Trees: 06 Prim’s Algorithm with a Matrix Example 1
Prims Algorithm to Find Minimum Spanning Tree of a Graph | Algorithm with Pseudo Code | Logic First
#2 Prims Algorithm Minimum | How to find Spanning Tree Greedy Search Algorithm by Dr. Mahesh Huddar
Lecture 96: Minimum Spanning Tree || Prim's Algorithm
How does Prim's Algorithm work? #shorts
Prim's Algorithm Part-1 For Minimum Spanning Tree Explained With Solved Example in Hindi
Комментарии
 0:20:12
0:20:12
 0:07:18
0:07:18
 0:22:08
0:22:08
 0:09:55
0:09:55
 0:14:53
0:14:53
 0:19:10
0:19:10
 0:13:02
0:13:02
 0:08:21
0:08:21
 0:10:48
0:10:48
 0:06:46
0:06:46
 0:13:15
0:13:15
 0:31:34
0:31:34
 1:22:10
1:22:10
 0:07:40
0:07:40
 0:04:33
0:04:33
 0:09:40
0:09:40
 0:07:31
0:07:31
 0:11:32
0:11:32
 0:04:56
0:04:56
 0:17:41
0:17:41
 0:05:42
0:05:42
 0:33:04
0:33:04
 0:00:49
0:00:49
 0:08:10
0:08:10