Prim's Algorithm for Minimum Spanning Trees (MST) | Graph Theory

We go over Prim's Algorithm, and how it works to find minimum spanning trees (also called minimum weight spanning trees or minimum cost spanning trees). We'll also see two examples of using Prim's algorithm to find minimum spanning trees in connected weighted graphs.

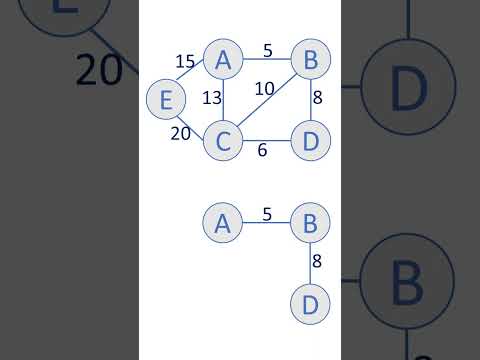
This algorithm is one way to solve the problem of finding a spanning tree of minimum weight in a connected weighted graph. The weight of a subgraph of a weighted graph is the sum of the weights of the subgraph's edges. So, among all spanning trees of a graph G, if we use Prim's algorithm to find a minimum spanning tree T of G, it will be a spanning tree of minimum weight/minimum cost. Note that neither spanning trees nor minimum spanning trees are necessarily unique.

#GraphTheory #Math

★DONATE★

Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!

Follow Wrath of Math on...

[WrathofMath]

Support the production of this course by joining Wrath of Math as a Channel Member for exclusive and early videos, original music, and upcoming lecture notes for the graph theory series! Plus your comments will be highlighted for me so it is more likely I'll answer your questions!

[jacobshin]

I love these graph videos from a mathematical perspective. There are way more computer science/interview prep videos all over youtube that don't explain WHY an algorithm works or graph property exists and not enough videos like these. Definitely looking forward to your future videos with the proofs.

[soroushfth]

this is the best playlist for graph theory, thank you so much

[mnnuila]

Yes CS perspective for all related videos

[AnselmoBattisti]

That was the clearest explanation of the Prim 's algorithm I already had in my life! Thanks!

[davidshi]

Haha, you always have a knack for covering topics that I just finished learning a month ago. Good video, though. It's also amusing to adapt Prim's to find the maximum spanning tree, and even minimum product spanning tree!

[tusharbarman]

thanks man for making a video on such a short time. Appreciate it

[mahmoudalbahar]

Please ... can you make video about the following question?
(What I found at internet is : cardinality of real irrational numbers is equal to cardinality of real numbers
so there must be bijection between them but I can't find it by myself or by internet)
The question is
what is the bijection between real irrational numbers and real numbers?

[anushaganesanpmp]

Could you tell when the proof of this algorithm would be explained as i am interested to know why does it work?

[maheshpatel]

Show that height of the cylinder of greatest volume which can be inscribed in a
right circular cone of height h and semi vertical angle α is one-third that of the
cone and the greatest volume of cylinder is
4πh³tan²α/27.
I just wanna know that how much do you rate this one out of 10 for difficulty?

[PunmasterSTP]

Anyone else wonder how things would have played out differently if Katniss hadn't volunteered?

[infinitymath]

Let T be a tree and e = (u, v) be an edge in T. Then beta(T.e) = beta(T. e), \\ beta(T)-1, \\ beta(T), otherwise.

if both u and v are stem vertices; if one of u and v is a leaf and other one is minor stem; otherwise.
Can you give me proof of this theorem??