filmov
tv
How to differentiate expression involving surd y=x√(x+1) using product rule

Показать описание
Given y = uv, where u = f(x) and v = g(x), then y' = u'v + uv'.
Some questions involving the product rule may also involve other rules, such as the chain rule.
In this example, we want the gradient function of y = x√(x+1).
Before differentiating, express the function using a fractional index to represent the surd.
y = x × (x+1)^(1/2). The function is a product of two simpler functions, hence the product rule is applied.
Let u = x and v = (x + 1)^(1/2). Then u' = 1 and v' = (1/2) × (x + 1)^(-1/2) × 1 [v' by the chain rule]
y' = u' × v + u × v' → y' = 1 × (x + 1)^(1/2) + x × (1/2) × (x + 1)^(-1/2)
After simplification, we have y' = (2x + 3) / (2√(x+1))
 0:13:51
0:13:51
 0:02:38
0:02:38
 0:03:16
0:03:16
 0:00:55
0:00:55
 0:11:45
0:11:45
 0:06:01
0:06:01
 0:00:43
0:00:43
 0:00:41
0:00:41
 0:02:44
0:02:44
 0:20:11
0:20:11
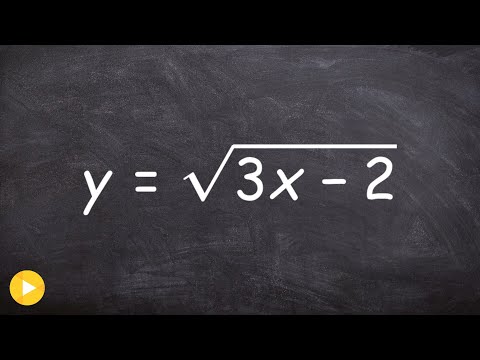 0:01:36
0:01:36
 0:05:21
0:05:21
 0:12:03
0:12:03
 0:52:51
0:52:51
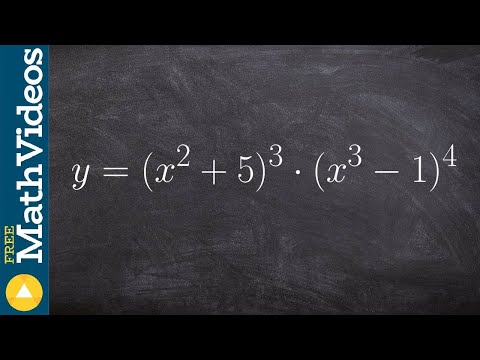 0:04:44
0:04:44
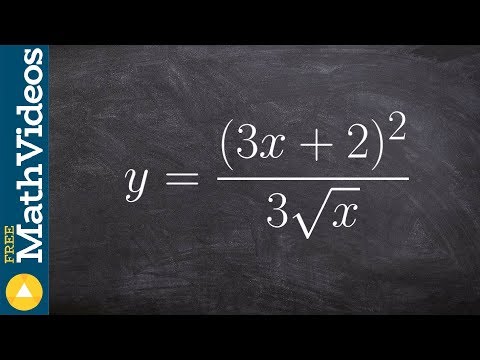 0:05:06
0:05:06
 0:04:54
0:04:54
 0:20:44
0:20:44
 0:00:43
0:00:43
 0:03:50
0:03:50
 0:00:51
0:00:51
 0:01:44
0:01:44
 0:10:58
0:10:58
 0:00:52
0:00:52