filmov
tv
Finding An Infinite Sum | Calculus
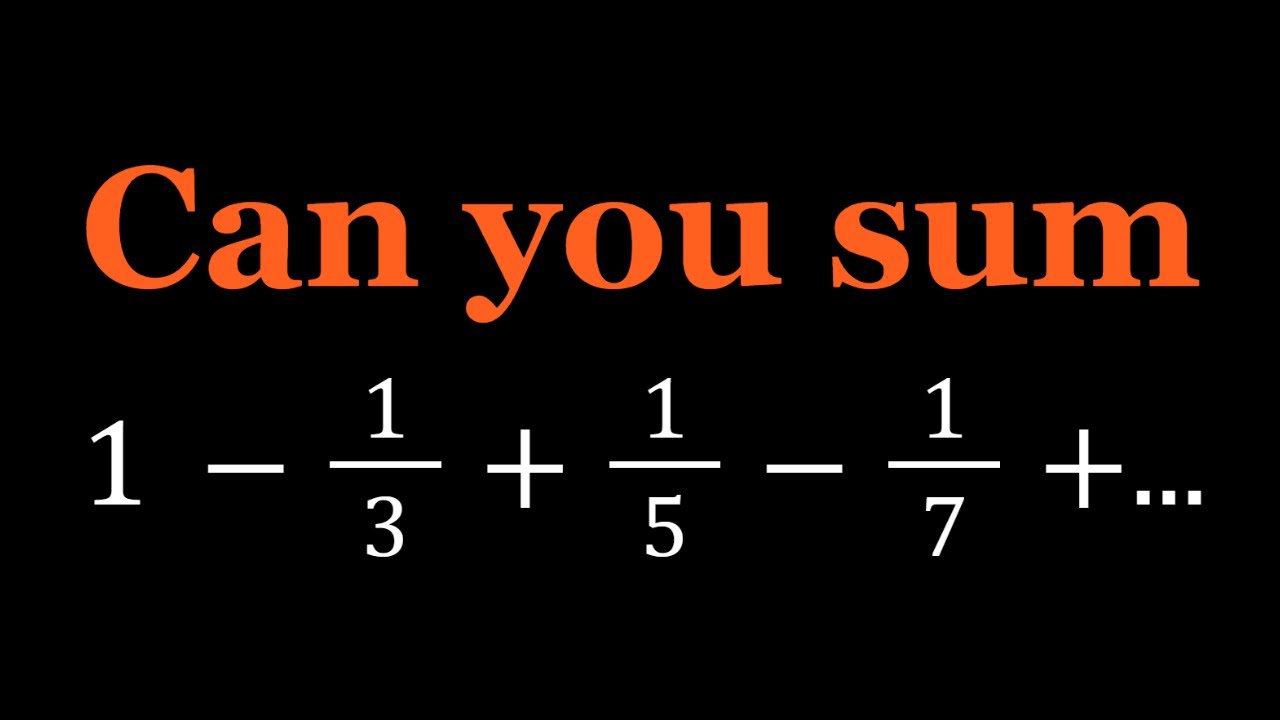
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #SequencesAndSeries #Calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #SequencesAndSeries #Calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Finding The Sum of an Infinite Geometric Series
Learning how to find the sum of an infinite geometric series
Finding An Infinite Sum | Calculus
Finding an infinite sum with triangles!
What's this infinite sum?
How to use the Integral Test to Approximate an Infinite Sum
Infinite series as limit of partial sums | Series | AP Calculus BC | Khan Academy
A visual infinite sum like you’ve never seen!
Mathematical Games Hosted by Ed Pegg Jr. [Episode 21: Ordering and Canonical Forms]
Evaluating the sum of an infinite series
How to determine the sum of a infinite geometric series
Infinite Geometric Series Sum
Infinite sum of powers of 4/9
Infinite sum of powers of sixths!
Sum of Infinite Series
[Complex Analysis] How to find the infinite sum of (i/3)^n
Find the Sum of the Infinite Geometric Series Harder Example!
Convergence and Divergence - Introduction to Series
Ex 1: Find the Sum of an Infinite Geometric Series
Alternating infinite sum!
Infinite Arithmetic
Infinite sum 1/n*(n+1)
Infinite Series - Numberphile
Ex 2: Find the Sum of an Infinite Geometric Series
Комментарии
 0:19:50
0:19:50
 0:02:08
0:02:08
 0:09:32
0:09:32
 0:01:00
0:01:00
 0:00:31
0:00:31
 0:03:32
0:03:32
 0:04:47
0:04:47
 0:00:57
0:00:57
 0:56:47
0:56:47
 0:02:01
0:02:01
 0:03:41
0:03:41
 0:00:45
0:00:45
 0:00:52
0:00:52
 0:00:55
0:00:55
 0:02:03
0:02:03
![[Complex Analysis] How](https://i.ytimg.com/vi/O53uYimtd2k/hqdefault.jpg) 0:01:07
0:01:07
 0:06:47
0:06:47
 0:16:18
0:16:18
 0:03:45
0:03:45
 0:00:52
0:00:52
 0:02:27
0:02:27
 0:00:46
0:00:46
 0:09:31
0:09:31
 0:03:59
0:03:59