filmov
tv
Calculus 1, Lecture 35: Derivatives & Integrals Final Exam Review Problems
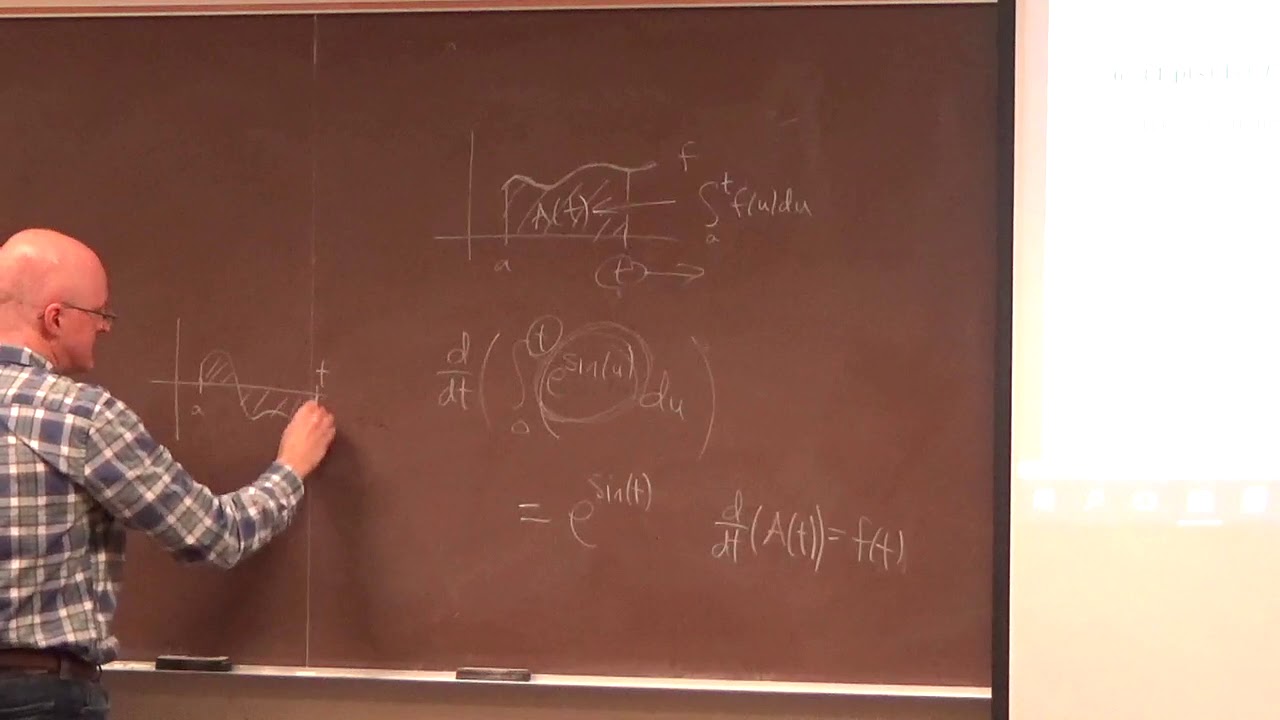
Показать описание
Calculus 1, Lecture 35. Final Exam Review.
(0:00) Mostly we'll go through Exam 3 problems (Main Topics: Optimization and Integration).
(1:25) Start going through Exam 3 problems, starting with multiple choice questions related to theorems and optimization.
(6:20) Fundamental Theorem of Calculus question.
(9:54) Linearity property of integrals.
(15:12) L'Hopital's Rule problem for a 0/0 indeterminate form.
(17:38) Optimization question: find the local extreme points, confirm with the First Derivative Test, with the Second Derivative Test, and then find the local extreme values (local max and local min values).
(21:10) Determine how a critical point and minimum value depend on parameters and confirm with the second derivative.
(26:25) Find the change in position with the Fundamental Theorem of Calculus when you know the velocity (the position function is also given).
(29:50) Related rates problem (sliding ladder).
(33:58) Minimize the surface area of a cylinder of fixed volume.
(36:10) Verify that a function solves a differential equation (or not).
(38:43) Decide where data are more dense based on a density function (DF) and then determine a cumulative percent with a cumulative distribution function (CDF).
(42:41) Graph a parametric curve (based on parametric equations), find the speed function, and estimate the distance traveled (with technology or with a right-hand Riemann sum).
(48:13) Given the graph of a flow rate, which is both positive and negative, and with areas labeled, us the Fundamental Theorem of Calculus to find the change in volume and the final volume.
(52:34) Prove that a function is constant using the Constant Function Theorem (and also given assumptions about two other related functions).
(56:13) Quick overview of Exams 1 and 2, including problems about the limit definition of the derivative.
(0:00) Mostly we'll go through Exam 3 problems (Main Topics: Optimization and Integration).
(1:25) Start going through Exam 3 problems, starting with multiple choice questions related to theorems and optimization.
(6:20) Fundamental Theorem of Calculus question.
(9:54) Linearity property of integrals.
(15:12) L'Hopital's Rule problem for a 0/0 indeterminate form.
(17:38) Optimization question: find the local extreme points, confirm with the First Derivative Test, with the Second Derivative Test, and then find the local extreme values (local max and local min values).
(21:10) Determine how a critical point and minimum value depend on parameters and confirm with the second derivative.
(26:25) Find the change in position with the Fundamental Theorem of Calculus when you know the velocity (the position function is also given).
(29:50) Related rates problem (sliding ladder).
(33:58) Minimize the surface area of a cylinder of fixed volume.
(36:10) Verify that a function solves a differential equation (or not).
(38:43) Decide where data are more dense based on a density function (DF) and then determine a cumulative percent with a cumulative distribution function (CDF).
(42:41) Graph a parametric curve (based on parametric equations), find the speed function, and estimate the distance traveled (with technology or with a right-hand Riemann sum).
(48:13) Given the graph of a flow rate, which is both positive and negative, and with areas labeled, us the Fundamental Theorem of Calculus to find the change in volume and the final volume.
(52:34) Prove that a function is constant using the Constant Function Theorem (and also given assumptions about two other related functions).
(56:13) Quick overview of Exams 1 and 2, including problems about the limit definition of the derivative.
Комментарии
 1:05:04
1:05:04
 0:36:22
0:36:22
 0:52:51
0:52:51
 0:03:38
0:03:38
 11:53:48
11:53:48
 0:55:58
0:55:58
 0:03:01
0:03:01
 6:38:13
6:38:13
 0:59:54
0:59:54
 0:04:35
0:04:35
 0:00:08
0:00:08
 0:00:13
0:00:13
 0:46:51
0:46:51
 0:11:23
0:11:23
 0:49:17
0:49:17
 0:00:10
0:00:10
 0:23:44
0:23:44
 0:00:27
0:00:27
 0:10:33
0:10:33
 0:21:58
0:21:58
 0:56:49
0:56:49
 0:05:24
0:05:24
 0:00:43
0:00:43
 0:00:29
0:00:29