filmov
tv
The Quadratic Formula No One Taught You

Показать описание
We derive an alternative version of the quadratic formula, then explore advantages and disadvantages of each version. This includes values for which they are defined, and the effect of rounding on the accuracy of solutions.
00:00 Intro
00:19 Derivation 1
02:29 Derivation 2
04:55 Problems with the original formula
07:40 Problems with the new formula
11:31 Comparison of accuracy
14:17 Why you should use both
00:00 Intro
00:19 Derivation 1
02:29 Derivation 2
04:55 Problems with the original formula
07:40 Problems with the new formula
11:31 Comparison of accuracy
14:17 Why you should use both
The Quadratic Formula No One Taught You
The Better Quadratic Formula You Won't Be Taught
How To Solve Quadratic Equations Using The Quadratic Formula
A Different Way to Solve Quadratic Equations
Learn How to Factor a Quadratic in Your Head When a is not Equal to One
Quadratic Formula Song
The simpler quadratic formula | Ep. 1 Lockdown live math
How to Solve Quadratic Equations using Three Methods - When Leading Coefficient is Not One
A Very nice Math Olympiad Question | find the integer solution of x | Algeria | Exponential equation
How to use the quadratic formula | Polynomial and rational functions | Algebra II | Khan Academy
Solving a quadratic equation when not equal to zero by factoring
Solving a quadratic when a is not equal to one
09 - The Quadratic Formula Explained, Part 1 (Practice Problems & Solutions)
GCSE Maths - Solving Quadratics Using the Quadratic Formula #51
Learn how to solve a quadratic equation by factoring when a is not equal to one
How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course
How to find the solutions of a quadratic using the quadratic formula
How To Determine The Discriminant of a Quadratic Equation
Ex 1: Factor and Solve a Quadratic Equation - a not 1
Determining the roots of a quadratic equation by factoring when a is not one
How to solve a quadratic when there are no solutions
Solving Quadratic Equations using Quadratic Formula - Quadratic Equations
How to Solve Quadratic Equations using the Quadratic Formula
How to apply the quadratic formula to find one solution
Комментарии
 0:18:16
0:18:16
 0:03:02
0:03:02
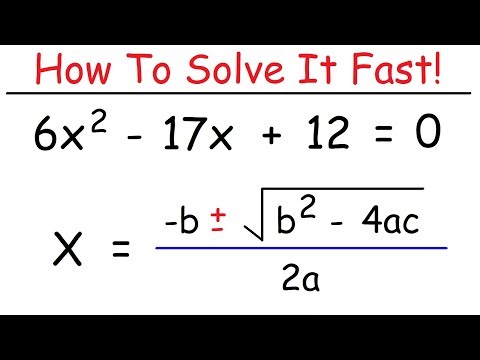 0:05:56
0:05:56
 0:03:49
0:03:49
 0:02:32
0:02:32
 0:02:19
0:02:19
 0:52:11
0:52:11
 0:15:43
0:15:43
 0:14:00
0:14:00
 0:16:32
0:16:32
 0:02:03
0:02:03
 0:04:48
0:04:48
 0:25:59
0:25:59
 0:05:27
0:05:27
 0:04:12
0:04:12
 0:12:29
0:12:29
 0:05:24
0:05:24
 0:03:05
0:03:05
 0:05:26
0:05:26
 0:06:03
0:06:03
 0:01:30
0:01:30
 0:09:06
0:09:06
 0:10:16
0:10:16
 0:02:29
0:02:29