filmov
tv
¿Puedes resolver el siguiente problema sin usar la calculadora? | (ARTIFICIOS ALGEBRAICOS) |

Показать описание
Calcular la raíz cuadrada de (20x21x22x23+1), usando artificios algebraicos, teoría de productos notables y cambio de variable.
#AcademiaInternet, #algebradesdecero
#AcademiaInternet, #algebradesdecero
¿Puedes resolver el siguiente problema geometrico de concurso?
¿Puedes resolver el siguiente problema de examen de admision?
¿Puedes resolver el siguiente problema de areas sombreadas? | [FIJA DE EXAMEN]
¿Puedes resolver el siguiente problema de geometria?
¿Puedes resolver el siguiente problema geométrico solo usando artificios geometricos?
¿Puedes resolver el siguiente problema de geometria? | [DEMOSTRACION DE FORMULA]
¿Puedes resolver el siguiente problema de areas sombreadas de concurso?
¿Puedes resolver el siguiente problema de triangulos?
ANUAL 2014 (ADUNI) - GEOMETRÍA (5° PARTE) - SAN MARCOS
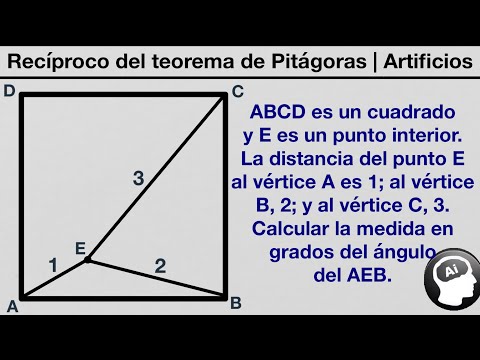
¿Puedes resolver el siguiente problema de olimpiadas matematicas? | Reciproco Teorema de Pitágoras
¿Puedes resolver el siguiente problema de aritmetica? | [CRIPTOARITMETICA]
¿Puedes resolver el siguiente problema de modelacion con parabolas? |
¿Puedes resolver el siguiente problema de funcion exponencial y modelado de poblacion? |
¿Puedes resolver el siguiente problema de geometria del espacio? | Solidos geometricos
¿Puedes resolver el siguiente problema de magnitudes directamente proporcionales?
¿Puedes resolver el siguiente problema de secundaria? | [90% NO RESPONDE] | (TRAZOS AUXILIARES)
¿Puedes resolver el siguiente problema sin usar la calculadora? | (ARTIFICIOS ALGEBRAICOS)
¿Puedes resolver el siguiente problema de areas sombreadas usando solo artificios geometricos?
¿Puedes resolver el siguiente reto matemático viral
PLANTEAR Y RESOLVER ECUACIONES LINEALES - Parte1 - Super fácil / Para principiantes
¿Puedes resolver el siguiente problema de areas sombreadas utilizando trazos auxiliares?
Truco resolver problemas Matemáticas transformando el problema con números más pequeños
¿Puedes RESOLVER este PROBLEMA de Matemáticas de secundaria?
¿PUEDES RESOLVER este PROBLEMA? | ECUACIÓN con EXPONENTES #1
Комментарии
 0:05:47
0:05:47
 0:05:55
0:05:55
 0:05:16
0:05:16
 0:07:33
0:07:33
 0:05:41
0:05:41
 0:07:27
0:07:27
 0:05:09
0:05:09
 0:05:14
0:05:14
 0:46:18
0:46:18
 0:07:59
0:07:59
 0:11:33
0:11:33
 0:08:48
0:08:48
 0:04:57
0:04:57
 0:06:04
0:06:04
 0:05:38
0:05:38
 0:06:37
0:06:37
 0:06:55
0:06:55
 0:05:29
0:05:29
 0:05:58
0:05:58
 0:03:37
0:03:37
 0:09:24
0:09:24
 0:05:55
0:05:55
 0:03:15
0:03:15
 0:12:18
0:12:18