filmov
tv
Find the limit of (sin(1/n) + sin(2/n) +...+sin(1))/n as n goes to infinity
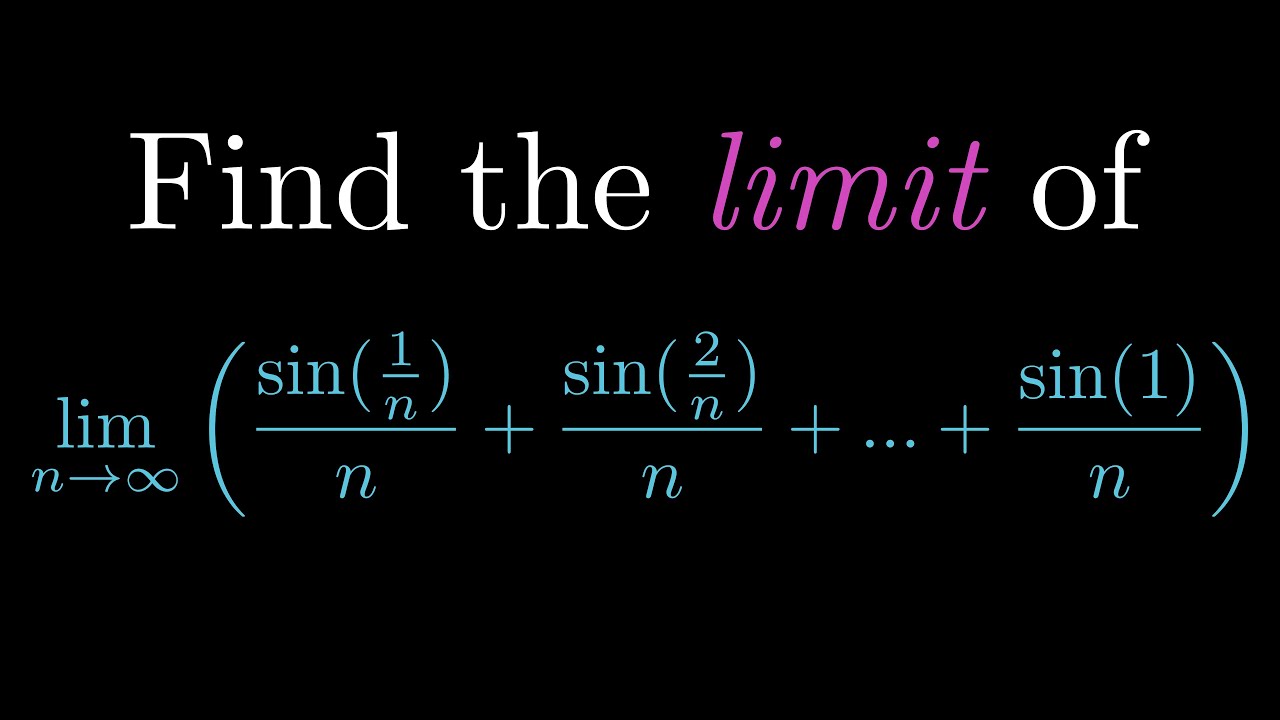
Показать описание
In this video we use Riemann sums to calculate the limit of the sum of sin(k/n) divided by to 1/n as n goes to infinity!
Limit of sin(1/x) as x approaches 0 Does Not Exist | Calculus 1 Exercises
Series of sin(1/n) diverges, Limit comparison test, calculus 2 tutorial
Limits of Trigonometric Functions
Find the limit of (sin(1/n) + sin(2/n) +...+sin(1))/n as n goes to infinity
How to Determine if a Sequence Converges or Diverges: Example with n*sin(1/n)
Calculus Made Easy: Limits of Sine Functions at Infinity: sin(1/x) and sin(1/n^2) Explained
LIMIT POINTS OF THE SET {1/n sin(1/n) : n in N}
Determine if series converges or diverges. {sin(1/n)}. Limit Comparison Test with harmonic series
The 5AM Premarket Routine That Made Me $1Million In Trading
Discover the Limit of x*sin(1/x) as x Approaches Infinity | Unraveling Calculus Mysteries 🧠📈🚀...
Limit Comparison Test for Sin(1/n)
How To Find The Limit At Infinity
Sum n=1 to infinity of sin(1/n^2)
Test the convergence of (sin(1/n))^2 using direct comparison, sin(1/n) less than 1/n trick.
The Sequence a_n = sin(n)/n Converges or Diverges Two Solutions with Proof
Limit of x*sin(1/x) as x approaches 0 | Calculus 1 Exercises
limit sin(1/x) as x goes to infinity, done in 25 seconds but in detail!
(Squeeze Thrm) Limit n goes to Infinity (sin(n))/n
Limit of sin(1/x) as x approaches to zero | What is the limit of sin (1/x)?
Series sin(1/n) diverges
Limit of x*sin(1/x) as x approaches Infinity | Calculus 1 Exercises
SQUEEZE THEOREM - The Setup
Determine if sequence converges or diverges. If converges find limit. {(n sin n)/(n^2 +1)}
Determine the convergence or divergence of the series n sin (1/n). Nth Term Test
Комментарии
 0:04:36
0:04:36
 0:05:36
0:05:36
 0:15:23
0:15:23
 0:02:53
0:02:53
 0:04:04
0:04:04
 0:01:51
0:01:51
 0:09:36
0:09:36
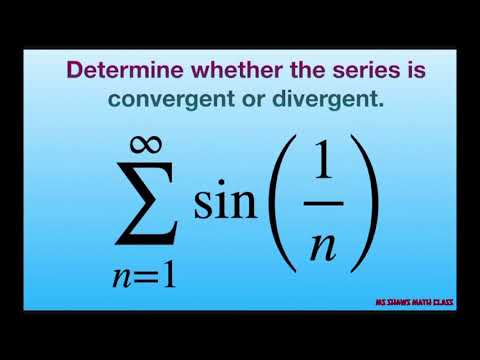 0:04:07
0:04:07
 0:26:25
0:26:25
 0:03:58
0:03:58
 0:16:22
0:16:22
 0:13:14
0:13:14
 0:01:12
0:01:12
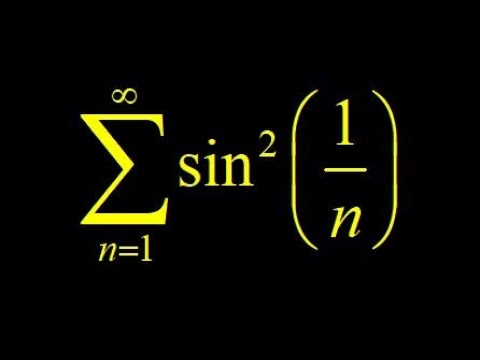 0:01:35
0:01:35
 0:02:47
0:02:47
 0:08:14
0:08:14
 0:00:29
0:00:29
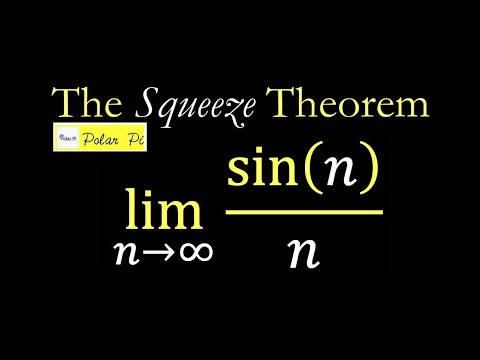 0:02:08
0:02:08
 0:11:50
0:11:50
 0:05:33
0:05:33
 0:09:23
0:09:23
 0:10:49
0:10:49
 0:02:18
0:02:18
 0:02:08
0:02:08