filmov
tv
Finding Even Larger Numbers

Показать описание
This is a follow-up to my last video about big numbers as there have been some new larger numbers discovered that can fit into a small space, like a text message. This is likely to be the final conclusion of the series unless something larger is proven.
Support me and innovative projects like these!
4D Golf
Music CC by 4.0
Jesse Spillane - An Undersea Cache of Relics
Evan Schaeffer - Blink
Support me and innovative projects like these!
4D Golf
Music CC by 4.0
Jesse Spillane - An Undersea Cache of Relics
Evan Schaeffer - Blink
Finding Even Larger Numbers
Tell if larger numbers are odd or even.
What is the largest even number that can be formed using the digits 1, 1, 2, 7 and 9 once?
Even and Odd Numbers - Math for Kids
How to find square root of even larger number
Largest 5-digit ODD/ EVEN number
Numberblocks are Under the Dirt! Learn Odd & Even Numbers | Playtime Learning
Largest ODD / EVEN 1-digit, 2-digit, 3-digit, 4-digit numbers @mathstubelearning123
Find the largest 6-digit EVEN number | Find the largest 6-digit ODD number @mathstubelearning123
Even and Odd Number | Quiz Time | Mathematics Quiz for Kids | @AAtoonsKids
Learn How to Identify Even Odd Numbers video for kids
How to find even number in big number
Largest ODD / EVEN 4-digit, 5-digit 6-digit numbers @mathstubelearning123
How to find odd and even numbers from a list of big numbers... | Smart Maths #maths #oddandeven
Find the Number of Positive 2-Digit Even Numbers With Distinct Digits
How Many Positive 2-Digit Even Numbers Are There?
Grade 2 Math 3.12b, Larger even or odd numbers (Part 2)
Identify Even and Odd Numbers | Find the Largest Number | Learn 1 to 20 | Homeschool for Toddlers
Python program to print the Largest Even and Largest Odd Number in a List
Math Lessons Finding the Missing Numbers, Odd and Even Numbers, Largest and Smallest
To find largest odd and even number in list
Find the largest even and odd numbers in a list (Python VEXCode VR)
The average of 5 consecutive even numbers is 40 what is the value of smallest of these numbers
How To Find EVEN & ODD Numbers? | Java Interview Question | #shorts #kiransir
Комментарии
 0:10:06
0:10:06
 0:05:57
0:05:57
 0:02:05
0:02:05
 0:04:53
0:04:53
 0:02:51
0:02:51
 0:00:19
0:00:19
 0:09:38
0:09:38
 0:03:41
0:03:41
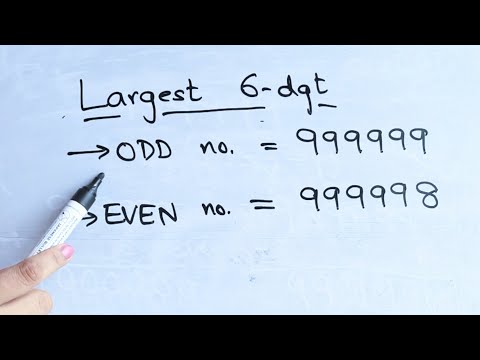 0:04:54
0:04:54
 0:10:55
0:10:55
 0:02:44
0:02:44
 0:00:47
0:00:47
 0:03:26
0:03:26
 0:01:00
0:01:00
 0:02:00
0:02:00
 0:01:47
0:01:47
 0:02:58
0:02:58
 0:08:23
0:08:23
 0:04:59
0:04:59
 0:06:01
0:06:01
 0:00:46
0:00:46
 0:01:02
0:01:02
 0:01:03
0:01:03
 0:01:00
0:01:00