filmov
tv
Solve a Logarithmic Equation Involving 2 Natural Logarithms Using the 1 to 1 Property of Logarithms
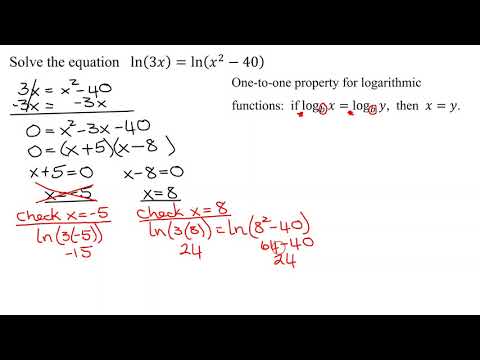
Показать описание
The equation to be solved is ln(3x)=ln(x^2-40). The one to one property of logarithms states that if log(base b) of x=log(base b) of y, then x=y. In this case, using the one to one property results in the quadratic equation 3x=x^2-40 that is then solved by factoring. After the solutions are found they are checked to see if they are extraneous solutions.
Timestamps
0:00 Introduction
0:57 One to One Property of Logarithms
2:00 Solve Quadratic Equation
3:30 Check for Extraneous Solutions
Timestamps
0:00 Introduction
0:57 One to One Property of Logarithms
2:00 Solve Quadratic Equation
3:30 Check for Extraneous Solutions
 0:25:27
0:25:27
 0:14:27
0:14:27
 0:00:55
0:00:55
 0:07:37
0:07:37
 0:07:08
0:07:08
 0:03:49
0:03:49
 0:00:58
0:00:58
 0:00:28
0:00:28
 0:00:58
0:00:58
 0:04:13
0:04:13
 0:06:02
0:06:02
 0:02:02
0:02:02
 0:02:49
0:02:49
 0:00:22
0:00:22
 0:05:47
0:05:47
 0:09:13
0:09:13
 0:01:33
0:01:33
 0:09:47
0:09:47
 0:00:35
0:00:35
 0:06:01
0:06:01
 0:08:09
0:08:09
 0:03:02
0:03:02
 0:03:27
0:03:27
 0:03:51
0:03:51