filmov
tv
Integral of cos(x) from 0 to infinity

Показать описание
In this problem I work out the integral of cos(x) from 0 to infinity. This is a problem from a very old book called Integral Calculus. It was written by H.B. Phillips and it was published in 1917.
(the above links are my affiliate links)
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
(the above links are my affiliate links)
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
Integral of cos(x) from 0 to infinity
Integral of cos(x)*cos^-1(x) from 0 to 1
integral of cos^-1(x) from 0 to 1/2
integrate y = cos x from x=0 to pi/2
Integral of cos(x) dx from 0 to pi/2 (Definite Integral)
How to Quickly Integrate Cos x and Sine x | Integral Calculus
Evaluate the Definite Integral (cos x) dx over [0, pi] using the Fundamental Theorem of Calculus
Integral cos(x)/cosh(x) from 0 to infinity
Multivariate Calculus Tutorial 6 - Parametrization and Line Integrals
Integral of cos(x^2) from 0 to infinity
Integral of cos^6(x) from 0 to pi/2.
cos x ki power 0 ka integration | Integration of cos x ki power 0 |
Improper integral e^-x*cos(x) on zero to infinity: integration by parts improper integral.
∫cos(x + cos(x)) dx [0, π]. MIT Integration Bee 2022 (Question 6, Qualifying Exam).
Integral of 1/(4-cos(x))^2 from 0 to pi
A fascinating holiday special: integral of e^cos(x) from 0 to pi/2
Integral from 0 to pi/2 of e^cos x sin x dx (U-substitution)
A beautiful result in calculus: Solution using complex analysis ( Integral cos(x)/(x^2+1) )
int cos(x)/cosh(x) from 0 to infinity: trigonometric functions unite!
Prove that integration of mod cos x from 0 to 2pie is equal to 4 | Math Integration vvi 12th Maths
How to integrate cos(x^2) - The Fresnel Integral C(x)
integral of cos^2(theta) from 0 to pi/2, calculus 2 tutorial
Evaluate integral cos x sin(sin x) dx over [0, pi/2]. The substitution rule for definite integrals
Contour Integral, General Case cos(ax)/(x^2+b^2), from 0 to infinity
Комментарии
 0:02:29
0:02:29
 0:06:54
0:06:54
 0:06:14
0:06:14
 0:00:39
0:00:39
 0:00:44
0:00:44
 0:01:00
0:01:00
 0:02:46
0:02:46
 0:12:31
0:12:31
 1:07:06
1:07:06
 0:06:20
0:06:20
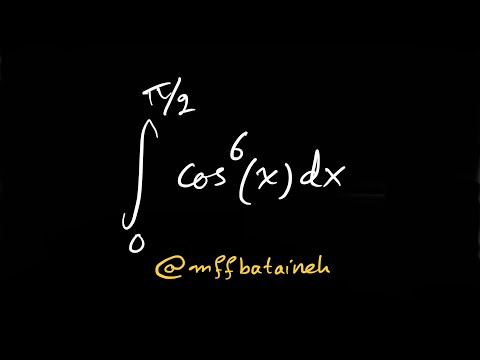 0:09:05
0:09:05
 0:06:18
0:06:18
 0:04:18
0:04:18
 0:01:01
0:01:01
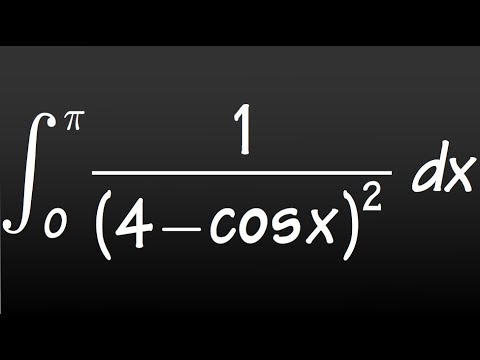 0:06:55
0:06:55
 0:14:58
0:14:58
 0:02:38
0:02:38
 0:16:40
0:16:40
 0:07:34
0:07:34
 0:08:04
0:08:04
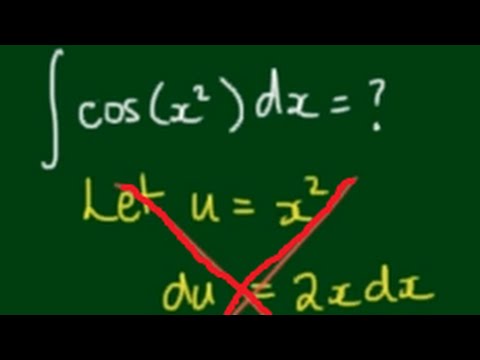 0:12:28
0:12:28
 0:02:45
0:02:45
 0:03:11
0:03:11
 0:03:23
0:03:23