filmov
tv
Integral of cos^6(x) from 0 to pi/2.
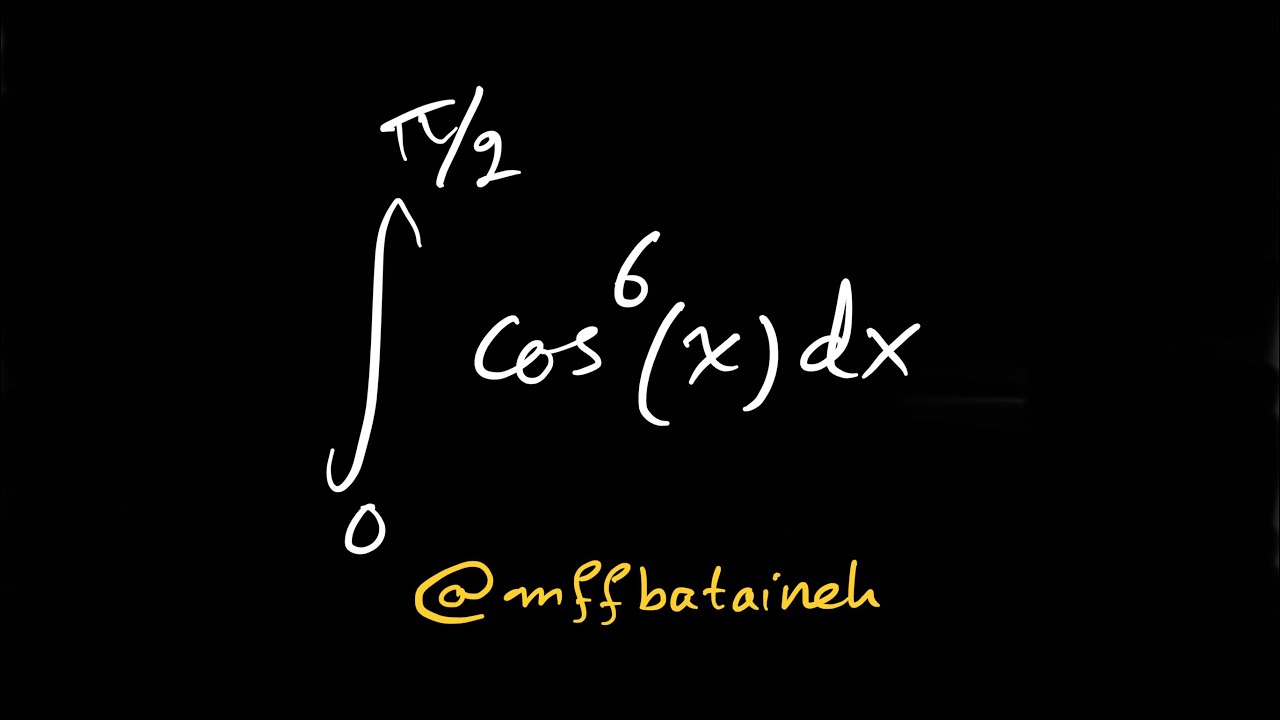
Показать описание
Integral of cos^6(x) from 0 to pi/2.
Integral of cos⁶(x) from 0 to π/2.
In this video, the host, Muhammad, walks viewers through the process of solving a definite integral problem. Specifically, the integral ∫ from 0 to π/2 of cosine^6(x) dx.
To solve this, he employs the strategy of rewriting the term cosine^6 in terms of cosines to the power one to facilitate easier integration. He benefits from the double angle formula for cosine, expressed as cosine^2 = 1 + cosine(2x)/2, and applies this formula to rewrite the original cosine^6 term. The integral then changes from a problem dealing with cosine^6 to one dealing with (1 + cosine(2x)/2)^3.
After using binomial expansion, simplifying terms, applying the double angle formula again to square terms and cube terms, and then further simplifying using the formula for the product of two cosines, Muhammad arrives at a simplified integrand that only contains cosine terms with power one. This allows for straightforward integration of each term.
When the definite integral is evaluated from 0 to π/2, most terms disappear as they result in sine functions with multiples of π, which are zero. The only remaining term after integration and evaluation is (5π)/32, which is the final solution to the original definite integral problem.
Throughout the video, Muhammad encourages viewers to try out the steps themselves, explains each step in detail, and uses clear visual cues to aid understanding. At the end, he invites viewers to like, subscribe, and click the bell icon to not miss future videos.
Integral of cos⁶(x) from 0 to π/2.
In this video, the host, Muhammad, walks viewers through the process of solving a definite integral problem. Specifically, the integral ∫ from 0 to π/2 of cosine^6(x) dx.
To solve this, he employs the strategy of rewriting the term cosine^6 in terms of cosines to the power one to facilitate easier integration. He benefits from the double angle formula for cosine, expressed as cosine^2 = 1 + cosine(2x)/2, and applies this formula to rewrite the original cosine^6 term. The integral then changes from a problem dealing with cosine^6 to one dealing with (1 + cosine(2x)/2)^3.
After using binomial expansion, simplifying terms, applying the double angle formula again to square terms and cube terms, and then further simplifying using the formula for the product of two cosines, Muhammad arrives at a simplified integrand that only contains cosine terms with power one. This allows for straightforward integration of each term.
When the definite integral is evaluated from 0 to π/2, most terms disappear as they result in sine functions with multiples of π, which are zero. The only remaining term after integration and evaluation is (5π)/32, which is the final solution to the original definite integral problem.
Throughout the video, Muhammad encourages viewers to try out the steps themselves, explains each step in detail, and uses clear visual cues to aid understanding. At the end, he invites viewers to like, subscribe, and click the bell icon to not miss future videos.
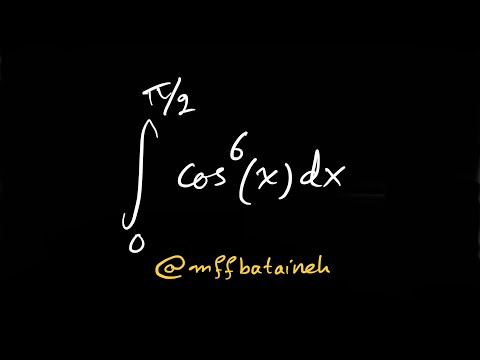 0:09:05
0:09:05
 0:05:39
0:05:39
 0:07:28
0:07:28
 0:05:42
0:05:42
 0:13:55
0:13:55
 0:03:06
0:03:06
 0:03:10
0:03:10
 0:11:08
0:11:08
 5:47:36
5:47:36
 0:31:29
0:31:29
 0:00:52
0:00:52
 0:02:16
0:02:16
 0:00:12
0:00:12
 0:03:24
0:03:24
 0:01:32
0:01:32
 0:03:01
0:03:01
 0:00:09
0:00:09
 0:09:26
0:09:26
 0:07:16
0:07:16
 0:15:54
0:15:54
 0:00:15
0:00:15
 0:00:17
0:00:17
 0:00:19
0:00:19
 0:00:23
0:00:23