filmov
tv
Linear Algebra: Transition Matrix

Показать описание
This videos explains how to find a transition matrix which translates coordinate vectors from a basis to a new basis in Euclidean vector spaces.
Linear Algebra: Transition Matrix
Transformation matrix with respect to a basis | Linear Algebra | Khan Academy
Change of basis | Chapter 13, Essence of linear algebra
Given two non standard bases, find transition matrices
Markov Chains & Transition Matrices
Change of Basis
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
The Transition Matrix
How to Find the Matrix of a Linear Transformation
Transition Matrices
How to Find Transition Matrix Between Bases | Linear Algebra Exercises
Change of basis matrix | Alternate coordinate systems (bases) | Linear Algebra | Khan Academy
Transition Matrix || Linear Algebra || Lecture-17
Markov Matrices
Linear Algebra Example Problems - Change of Coordinates Matrix #2
Transition matrix | Change of basis matrix|how do you find the transition matrix
Matrix Transformations : reflections and rotations
Problem 1 on State Transition Matrix
Matrix with respect to a basis
Transition Matrix for Axes Rotation in 3D and 2D | Linear Algebra
Change of basis - transformation matrices
Finding and using the matrix of a linear transformation relative to non standard bases
Markov Chains Clearly Explained! Part - 1
Комментарии
 0:08:45
0:08:45
 0:18:02
0:18:02
 0:12:51
0:12:51
 0:10:45
0:10:45
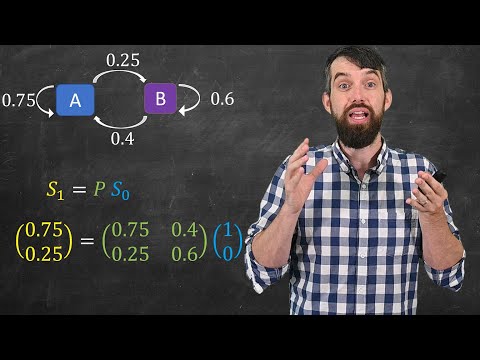 0:06:54
0:06:54
 0:09:34
0:09:34
 0:10:59
0:10:59
 0:13:52
0:13:52
 0:13:03
0:13:03
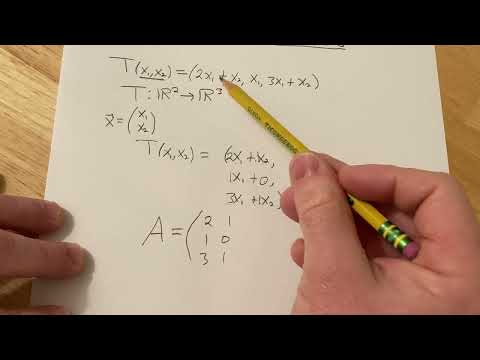 0:05:19
0:05:19
 0:05:16
0:05:16
 0:06:51
0:06:51
 0:17:55
0:17:55
 0:18:00
0:18:00
 0:11:49
0:11:49
 0:10:47
0:10:47
 0:11:53
0:11:53
 0:03:26
0:03:26
 0:10:32
0:10:32
 0:15:06
0:15:06
 0:13:17
0:13:17
 0:20:48
0:20:48
 0:09:29
0:09:29
 0:09:24
0:09:24