filmov
tv
Introduction to the Multinomial Distribution

Показать описание
An introduction to the multinomial distribution, a common discrete probability distribution. I discuss the basics of the multinomial distribution and work through two examples of probability calculations. For comparison purposes, I finish off with a quick example of a multivariate hypergeometric probability calculation.
Introduction to the Multinomial Distribution
What Is The Multinomial Probability Distribution Formula Example Explained
The Multinomial Distribution : Data Science Basics
Introduction to Multinomial Probabilities
SOR1020: The multinomial distribution
L04.9 Multinomial Probabilities
Multinomial Distribution: Introduction and Example
[5. Multiple RVs] 5.8 The Multinomial Distribution
Introduction to Probability: The Multinomial Distribution
Multinomial Distribution | Intuition & Introduction | example in TensorFlow Probability
Multinomial Probability Distribution
Multinomial Distribution
Multinomial distribution
Probability Adventures #24 The Multinomial Distribution
(STa40) The Hypergeometric, N. Binomial, & Multinomial Distributions
Multinomial Distribution, Clearly Explained!! (2022) | Statistics Tutor
Multinomial Distribution
Video 26, Theory and Example, Multinomial Distribution, 1 of 1
What are the Bernoulli, binomial, and multinomial Distributions?
An Introduction to the Binomial Distribution
Multinomial Distribution (Explanation) Part 1
GLM - Multinomial Regression (1/3) - Intro
Tutorial 40: Multinomial Distribution in Probability
The Multinomial Coefficient
Комментарии
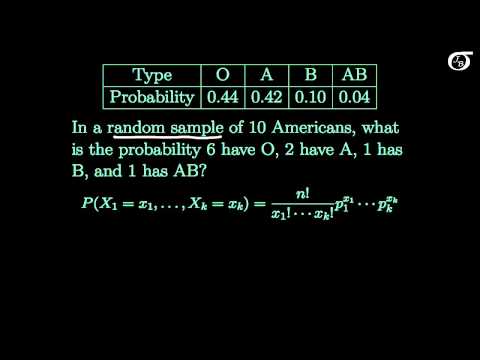 0:11:15
0:11:15
 0:04:59
0:04:59
 0:21:38
0:21:38
 0:05:35
0:05:35
 0:08:33
0:08:33
 0:10:36
0:10:36
 0:06:42
0:06:42
![[5. Multiple RVs]](https://i.ytimg.com/vi/_nb11h2pabo/hqdefault.jpg) 0:04:48
0:04:48
 0:08:12
0:08:12
 0:12:56
0:12:56
 0:07:07
0:07:07
 0:06:14
0:06:14
 0:17:36
0:17:36
 0:18:41
0:18:41
 0:28:41
0:28:41
 0:01:49
0:01:49
 0:08:12
0:08:12
 0:12:23
0:12:23
 0:00:47
0:00:47
 0:14:11
0:14:11
 0:10:00
0:10:00
 0:04:23
0:04:23
 0:09:46
0:09:46
 0:07:50
0:07:50