filmov
tv
What Is The Multinomial Probability Distribution Formula Example Explained

Показать описание
In this video we discuss what is the multinomial probability distribution and how and when to use it. We also cover the multinomial distribution formula and go through an example in depth.
Transcript/notes
Multinomial distribution
A binomial distribution is based on a probability experiment with a fixed number of trials with each trial only having 2 possible outcomes.
A multinomial distribution, which is a type of discrete probability distribution, is based on a probability experiment where each trial has more than 2 outcomes.
For instance, a person may have a choice of what to watch on TV, a drama, a horror flick, a romance, an action movie, or a documentary.
There are 4 requirements for a multinomial experiment. Number 1 is that there must be a fixed number of trails. Number 2 is that each trial has a specific number of outcomes. Number 3 is that each trial must be independent of one another, and number 4 is that the probability of a particular outcome remains the same.
The formula for the multinomial distribution is probability of x equals, n factorial divided by x1 factorial times x2 factorial times x3 factorial and so on to xK factorial, times p1 to the x1 times p2 to the x2 and so on to pk to the xK. And x1 plus x2 plus x3, so on to xK equals n, and p1 plus p2 plus p3 so on to pK equals 1.
Ok, a lot to unpack here, but it is actually easier than you may think. In this formula, probability of x consists of several events, e1, e2, e3 and so on. And the x’s represent the number of times each of the different events occurs, so x1 represents the number of times event 1 or e1 will occur. And p represents the probabilities of each of those events and n is equal to the total number of occurrences of those events. So, if we had 3 events, e1, 2 and 3, and event 1 occurred 3 times, event 2 occurred 4 times and event 3 occurred once, x1 equals 3, x2 would equal 4 and x3 would equal 1, and n would be the total number of occurrences of those events, 3 plus 4 plus 1, which equals 8, and this is the number of trials.
Let’s look at an example. Lets say that you gathered data about people going to a fitness center, and found that 20% were doing strength training, 40% were doing cardio, 15% were doing yoga, and 25% were playing a sport. If 8 people walk into the fitness center, what is the probability that 1 of them is there to do strength training, 4 of them are there to do cardio, 1 of them is there to do yoga, and 2 of them are there to play a sport?
First, let’s unpack the question. We have 4 different activities, strength training, cardio, yoga and sports. So, these activities are the different events, e1 though e4. In the formula, the x’s represent the number of times each of the different events occurs, so x1 represents the number of times event 1 or e1 will occur, which in this case is strength training, and the question says 1 of them is there to do strength training, so our x1 value is 1. X2 represents event 2, which is cardio, and the question says 4 of them are there to do cardio, so, our x2 values is 3.
X3 represents event 3, which is yoga, and the question says 1 of them is there to do yoga, so our x3 value is 1. And x4 represents event 4, which is play a sport, and the question says, 2 of them are there to play a sport, so, the x4 value is 2.
Now that we have all of the x’s assigned values, we can sum them up, and that totals 8, which is the n value in the formula. And the p values, the probability values of each of the 4 different events was given in the question, for event 1, strength training, the probability is 20% or 0.20, which equals p1, for event 2, cardio the probability is 0.40, which equals p2, for event 3, yoga, the probability is 0.15 which equals p3, and for event 4, play a sport, the probability is 0.25, which equals p4.
Now we have all we need to plug and calculate. So, the probability of x, or the probability that 1 is there for strength training, 4 are there for cardio, 1 is there for yoga, and 2 are there to play a sport, equals, n factorial, which is 8 factorial divided by 1 factorial, times 4 factorial times 1 factorial, times 2 factorial, times 0.20 to the 1, times 0.40 to the 4, times 0.15 to the 1, times 0.25 squared.
Now we can calculate out, which I have done on the screen and we get a probability of 4%.
To sum this up, there is a 4% probability that if 8 people walk into a fitness center, 1 of them is there for strength training, 4 of them are there for cardio, 1 of them are there for yoga, and 2 of them are there to play a sport.
Timestamps
0:00 Multinomial Vs Binomial Distributions
0:25 4 Requirements For Multinomial Distribution
0:41 Formula For Multinomial Distribution
1:17 Formula explained in depth
2:01 Example Problem For Multinomial Distribution
Transcript/notes
Multinomial distribution
A binomial distribution is based on a probability experiment with a fixed number of trials with each trial only having 2 possible outcomes.
A multinomial distribution, which is a type of discrete probability distribution, is based on a probability experiment where each trial has more than 2 outcomes.
For instance, a person may have a choice of what to watch on TV, a drama, a horror flick, a romance, an action movie, or a documentary.
There are 4 requirements for a multinomial experiment. Number 1 is that there must be a fixed number of trails. Number 2 is that each trial has a specific number of outcomes. Number 3 is that each trial must be independent of one another, and number 4 is that the probability of a particular outcome remains the same.
The formula for the multinomial distribution is probability of x equals, n factorial divided by x1 factorial times x2 factorial times x3 factorial and so on to xK factorial, times p1 to the x1 times p2 to the x2 and so on to pk to the xK. And x1 plus x2 plus x3, so on to xK equals n, and p1 plus p2 plus p3 so on to pK equals 1.
Ok, a lot to unpack here, but it is actually easier than you may think. In this formula, probability of x consists of several events, e1, e2, e3 and so on. And the x’s represent the number of times each of the different events occurs, so x1 represents the number of times event 1 or e1 will occur. And p represents the probabilities of each of those events and n is equal to the total number of occurrences of those events. So, if we had 3 events, e1, 2 and 3, and event 1 occurred 3 times, event 2 occurred 4 times and event 3 occurred once, x1 equals 3, x2 would equal 4 and x3 would equal 1, and n would be the total number of occurrences of those events, 3 plus 4 plus 1, which equals 8, and this is the number of trials.
Let’s look at an example. Lets say that you gathered data about people going to a fitness center, and found that 20% were doing strength training, 40% were doing cardio, 15% were doing yoga, and 25% were playing a sport. If 8 people walk into the fitness center, what is the probability that 1 of them is there to do strength training, 4 of them are there to do cardio, 1 of them is there to do yoga, and 2 of them are there to play a sport?
First, let’s unpack the question. We have 4 different activities, strength training, cardio, yoga and sports. So, these activities are the different events, e1 though e4. In the formula, the x’s represent the number of times each of the different events occurs, so x1 represents the number of times event 1 or e1 will occur, which in this case is strength training, and the question says 1 of them is there to do strength training, so our x1 value is 1. X2 represents event 2, which is cardio, and the question says 4 of them are there to do cardio, so, our x2 values is 3.
X3 represents event 3, which is yoga, and the question says 1 of them is there to do yoga, so our x3 value is 1. And x4 represents event 4, which is play a sport, and the question says, 2 of them are there to play a sport, so, the x4 value is 2.
Now that we have all of the x’s assigned values, we can sum them up, and that totals 8, which is the n value in the formula. And the p values, the probability values of each of the 4 different events was given in the question, for event 1, strength training, the probability is 20% or 0.20, which equals p1, for event 2, cardio the probability is 0.40, which equals p2, for event 3, yoga, the probability is 0.15 which equals p3, and for event 4, play a sport, the probability is 0.25, which equals p4.
Now we have all we need to plug and calculate. So, the probability of x, or the probability that 1 is there for strength training, 4 are there for cardio, 1 is there for yoga, and 2 are there to play a sport, equals, n factorial, which is 8 factorial divided by 1 factorial, times 4 factorial times 1 factorial, times 2 factorial, times 0.20 to the 1, times 0.40 to the 4, times 0.15 to the 1, times 0.25 squared.
Now we can calculate out, which I have done on the screen and we get a probability of 4%.
To sum this up, there is a 4% probability that if 8 people walk into a fitness center, 1 of them is there for strength training, 4 of them are there for cardio, 1 of them are there for yoga, and 2 of them are there to play a sport.
Timestamps
0:00 Multinomial Vs Binomial Distributions
0:25 4 Requirements For Multinomial Distribution
0:41 Formula For Multinomial Distribution
1:17 Formula explained in depth
2:01 Example Problem For Multinomial Distribution
Комментарии
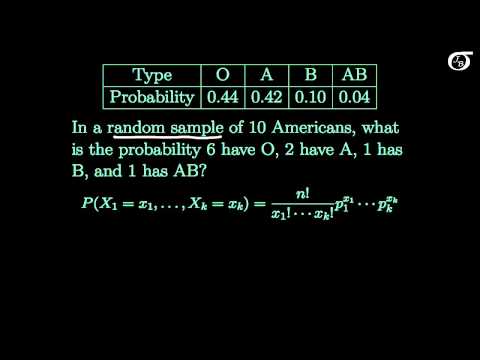 0:11:15
0:11:15
 0:04:59
0:04:59
 0:05:35
0:05:35
 0:10:36
0:10:36
 0:16:32
0:16:32
 0:21:38
0:21:38
 0:07:07
0:07:07
 0:12:34
0:12:34
 0:18:41
0:18:41
![[5. Multiple RVs]](https://i.ytimg.com/vi/_nb11h2pabo/hqdefault.jpg) 0:04:48
0:04:48
 0:08:01
0:08:01
 0:08:12
0:08:12
 0:04:29
0:04:29
 0:09:46
0:09:46
 0:08:33
0:08:33
 0:08:46
0:08:46
 0:07:10
0:07:10
 0:12:56
0:12:56
 0:06:13
0:06:13
 0:06:14
0:06:14
 0:07:33
0:07:33
 0:20:27
0:20:27
 0:00:47
0:00:47
 0:06:21
0:06:21