ODE | Bifurcation diagrams

Examples and explanations for a course in ordinary differential equations.

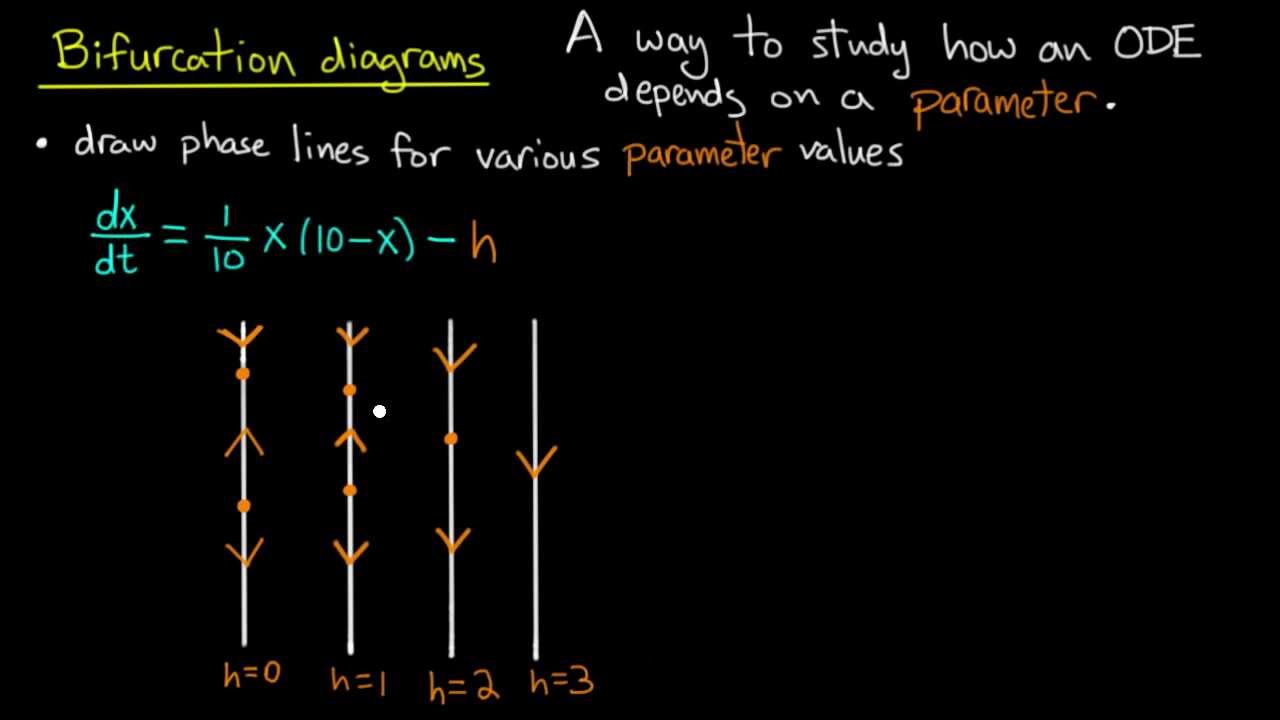
In this video we explain how to construct a bifurcation diagram for a differential equation that depends on a parameter. We illustrate the idea using the example of the logistic equation with a harvesting parameter. We also show how the bifurcation diagram can be used to answer questions about harvesting rates.

[jackbequick]

It's been 7 years, but it's an amazing video still. Great quality for a 2012!

[ledk]

Look at the parabola as a normal function with 'h' as dependent and 'x' as independent variable h = (1/10)*x*(10 - x). As you want to find out the top of the parabola (critical point) you have to take the derivative of that function and look where it is 0 --> dh/dx = 0 = 1 - 0.2x. solve this and you get 5 for x. put this into original parabola equation and solve for h. --> Result = h = 2.5

[sahirnagpal]

I don't think that there's only one point at h = 2.
There is only one point at h = 2.5

[Pinktree]

Currently studying Pure Maths and took a ODE math course as a bit of change of pace.... Thanks for your videos, you explained it more simply and more to the point than my professor

[kankyu]

Thank you, this is really clear, finally understand what a bifurcation diagram is. Before I was taught this, but never could wrap my head around what the curves meant. Thanks for the video.

[eivindfosse]

You have some of the best math tutoring videos out there man :) Keep up the good work!

[ChathuraJayalath]

This is the best video tutorial for Bifurcations

[nikirick]

There are two equilibrium points for h=2...x=5+-sqrt5

[pauluk]

An interesting question: the answer is h = 2 (per unit time) of course, because that's level at which population declines - from any starting number whatsoever - in this fishery. Its rather counter intuitive, that, because we think there's a vast difference between 2 fish and 2 million fish in terms of restocking. But the model doesn't lie.

There's a slip at 1:45 We should have: x = 5 ± √15 and, more generally, all solutions are of the form: x = 5 ± √(25 - 10h), which makes it clear, I think.

[jackpistone]

pretty sure its supposed to be 5 +/- sqrt(15) not sqrt(10)

[FabboS]

What a great video to understand this topic. Thanks a lot.

[pauluk]

It's important to distinguish between the fish numbers (x) and the harvesting (h) - which is a parameter and not therefore directly related to x. Any level of x above the lower limb gives a growing pop. (so 'x=5' is the pop. for 'maximal' growth). But '5' is critical when we're around the limit for 'h' because the pop. (if correctly harvested) won't then change. The 'peak' rate at the top of the parabola has dropped to 'zero' and you have a 'large', pop. but it's on the verge of 'collapse'.

[tomimn]

...okay, so a rate of 2.5 fish can be harvested without bringing the fish to extinction, assuming that the initial fish population is at above equilibrium. am I getting it right?

[ricardoa]

This is awesome, looking forward to seeing it soon.
Thank you again!

[InfinityOver]

Excellent, to this day people like me are using these videos.

[mathintro]

Hello.i hope you'd be able to read this. Do you know about two parameter bifurcation? Can you suggest a book that I could read? Thanks

[ricardoa]

Thank you very much for all your videos, they are all very helpful. Since you are now focusing on ODE's, could you do some videos in Sturm-Liouville and Differential operators theory?
Thank you very much.

[yzhang]

This might be a stupid question: why did u go positive rather than negative when testing h values? thanks

[randompotato]

did you mean the point at where there is only one equilibrium point is h=2.5 because when h=2.5 the differential becomes -(x-5)²/10 so dx/dt=0 have 2 times the solution x=5

[pauluk]

And I should say by " The 'peak' rate at the top of the parabola has dropped to 'zero' " I mean 'after allowing for harvesting' - so the height of the parabola (addition by growth) is '2.5' but the harvesting (removal) is '2.5' also. The 'zero' is really a 'population balance' not a 'static' population of individuals.