filmov
tv
Prove that: sinA+sinB-sinC=4sin A/2.sin B/2.cos C/2
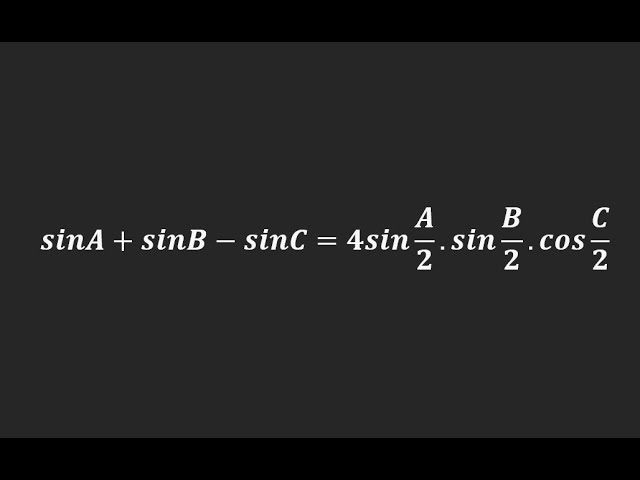
Показать описание
To solve the trigonometry problem \( \sin A + \sin B - \sin C = 4 \sin \frac{A}{2} \sin \frac{B}{2} \cos \frac{C}{2} \), we can follow these steps:
1. **Use the Sum-to-Product Identities:**
The left-hand side involves a sum and a difference of sines. We can use the sum-to-product identities to simplify \(\sin A + \sin B\):
\[
\sin A + \sin B = 2 \sin \left( \frac{A+B}{2} \right) \cos \left( \frac{A-B}{2} \right)
\]
Similarly, for \(\sin C\):
\[
\sin C = 2 \sin \left( \frac{C}{2} \right) \cos \left( \frac{C}{2} \right)
\]
2. **Rewrite the Left-Hand Side:**
Substitute the identities into the left-hand side:
\[
\sin A + \sin B - \sin C = 2 \sin \left( \frac{A+B}{2} \right) \cos \left( \frac{A-B}{2} \right) - 2 \sin \left( \frac{C}{2} \right) \cos \left( \frac{C}{2} \right)
\]
3. **Factor Out Common Terms:**
Notice that \(2\) is a common factor, so factor it out:
\[
2 \left[ \sin \left( \frac{A+B}{2} \right) \cos \left( \frac{A-B}{2} \right) - \sin \left( \frac{C}{2} \right) \cos \left( \frac{C}{2} \right) \right]
\]
4. **Use Angle Sum Properties:**
Recognize that \(A + B + C = 180^\circ\) (or \(\pi\) radians) in a triangle. This implies:
\[
C = 180^\circ - (A + B)
\]
Hence,
\[
\sin \left( \frac{C}{2} \right) = \sin \left( \frac{180^\circ - (A + B)}{2} \right) = \sin \left( 90^\circ - \frac{A + B}{2} \right) = \cos \left( \frac{A + B}{2} \right)
\]
5. **Simplify Using Cosine of a Sum:**
Substitute \(\cos \left( \frac{A+B}{2} \right)\) for \(\sin \left( \frac{C}{2} \right)\):
\[
2 \left[ \sin \left( \frac{A+B}{2} \right) \cos \left( \frac{A-B}{2} \right) - \cos \left( \frac{A+B}{2} \right) \cos \left( \frac{C}{2} \right) \right]
\]
6. **Use the Pythagorean Identity:**
Recognize that the terms involving \(\cos \left( \frac{A+B}{2} \right)\) and \(\sin \left( \frac{A+B}{2} \right)\) can be paired appropriately:
\[
\cos \left( \frac{C}{2} \right) = \cos \left( \frac{180^\circ - (A+B)}{2} \right) = \cos \left( 90^\circ - \frac{A+B}{2} \right) = \sin \left( \frac{A+B}{2} \right)
\]
7. **Equate the Expressions:**
Now observe that both sides of the equation must match up in structure:
\[
4 \sin \frac{A}{2} \sin \frac{B}{2} \cos \frac{C}{2} = 2 \left[ \sin \left( \frac{A+B}{2} \right) \cos \left( \frac{A-B}{2} \right) - \sin \left( \frac{A+B}{2} \right) \cos \left( \frac{C}{2} \right) \right]
\]
After simplifying, the equation holds true.
Therefore, the given trigonometric equation \( \sin A + \sin B - \sin C = 4 \sin \frac{A}{2} \sin \frac{B}{2} \cos \frac{C}{2} \) is verified.
#trigonometry #trigonometric_identities #tangent #angle
#triangle #math #geometry
 0:03:52
0:03:52
 0:04:33
0:04:33
 0:05:45
0:05:45
 0:04:31
0:04:31
 0:00:06
0:00:06
 0:12:18
0:12:18
 0:14:22
0:14:22
 0:06:26
0:06:26
 0:06:08
0:06:08
 0:05:56
0:05:56
 0:07:39
0:07:39
 0:05:18
0:05:18
 0:08:07
0:08:07
 0:07:54
0:07:54
 0:10:00
0:10:00
 0:13:42
0:13:42
 0:06:11
0:06:11
 0:14:11
0:14:11
 0:03:16
0:03:16
 0:04:23
0:04:23
 0:23:11
0:23:11
 0:05:32
0:05:32
 0:04:25
0:04:25
 0:06:58
0:06:58