filmov
tv
Prove that: sinA-sinB+sinC=4sin A/2.cos B/2.sin C/2

Показать описание
To solve the equation \(\sin A - \sin B + \sin C = 4 \sin \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}\), follow these steps:
### Step 1: Use Trigonometric Identities
Recall the sum-to-product identities:
- \(\sin x - \sin y = 2 \cos \left(\frac{x + y}{2}\right) \sin \left(\frac{x - y}{2}\right)\)
- \(\sin x + \sin y = 2 \sin \left(\frac{x + y}{2}\right) \cos \left(\frac{x - y}{2}\right)\)
### Step 2: Apply the Identities
Apply the identity for \(\sin A - \sin B\):
\[
\sin A - \sin B = 2 \cos \left(\frac{A + B}{2}\right) \sin \left(\frac{A - B}{2}\right)
\]
Thus, the equation becomes:
\[
2 \cos \left(\frac{A + B}{2}\right) \sin \left(\frac{A - B}{2}\right) + \sin C = 4 \sin \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}
\]
### Step 3: Transform \(\sin C\)
Use the double-angle identity for \(\sin C\):
\[
\sin C = 2 \sin \frac{C}{2} \cos \frac{C}{2}
\]
So, the equation now looks like:
\[
2 \cos \left(\frac{A + B}{2}\right) \sin \left(\frac{A - B}{2}\right) + 2 \sin \frac{C}{2} \cos \frac{C}{2} = 4 \sin \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}
\]
### Step 4: Factor Out Common Terms
Factor out \(2 \sin \frac{C}{2}\) on both sides of the equation:
\[
2 \cos \left(\frac{A + B}{2}\right) \sin \left(\frac{A - B}{2}\right) + 2 \sin \frac{C}{2} \cos \frac{C}{2} = 4 \sin \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}
\]
\[
2 \left( \cos \left(\frac{A + B}{2}\right) \sin \left(\frac{A - B}{2}\right) + \sin \frac{C}{2} \cos \frac{C}{2} \right) = 4 \sin \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}
\]
### Step 5: Simplify the Equation
Divide both sides by 2:
\[
\cos \left(\frac{A + B}{2}\right) \sin \left(\frac{A - B}{2}\right) + \sin \frac{C}{2} \cos \frac{C}{2} = 2 \sin \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}
\]
### Step 6: Equate Like Terms
Compare the terms involving \(\sin \frac{C}{2}\):
\[
\cos \left(\frac{A + B}{2}\right) \sin \left(\frac{A - B}{2}\right) = 2 \sin \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2} - \sin \frac{C}{2} \cos \frac{C}{2}
\]
Factor out \(\sin \frac{C}{2}\):
\[
\cos \left(\frac{A + B}{2}\right) \sin \left(\frac{A - B}{2}\right) = \sin \frac{C}{2} (2 \sin \frac{A}{2} \cos \frac{B}{2} - \cos \frac{C}{2})
\]
### Step 7: Solve for the Variables
At this point, you will need to consider specific values or relationships among \(A\), \(B\), and \(C\) to solve for these variables. You can analyze special cases or use numerical methods to find exact solutions. In general, trigonometric equations might have multiple solutions depending on the specific values of \(A\), \(B\), and \(C\).
### Conclusion
The process involves applying trigonometric identities, simplifying the equation, and equating like terms. Further steps would depend on the specific values or relationships between \(A\), \(B\), and \(C\) to find explicit solutions.
#trigonometry #trigonometric_identities #tangent #angle
#triangle #math #geometry
Комментарии
 0:04:31
0:04:31
 0:05:45
0:05:45
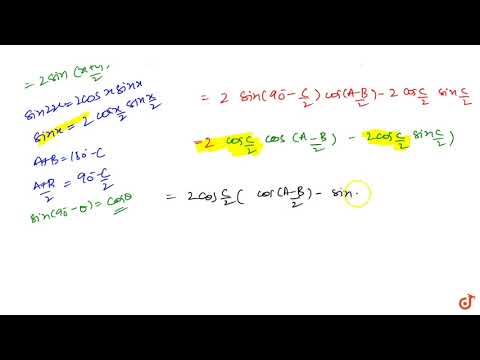 0:04:33
0:04:33
 0:03:52
0:03:52
 0:12:18
0:12:18
 0:06:08
0:06:08
 0:14:22
0:14:22
 0:05:56
0:05:56
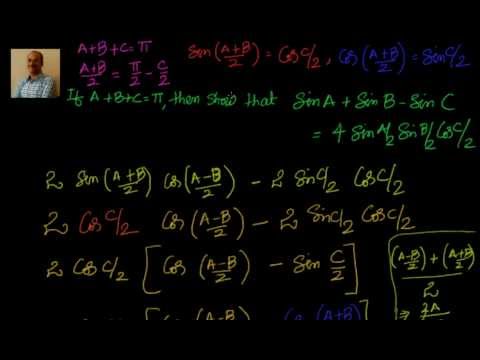 0:06:26
0:06:26
 0:00:06
0:00:06
 0:06:11
0:06:11
 0:05:02
0:05:02
 0:07:39
0:07:39
 0:05:18
0:05:18
 0:07:54
0:07:54
 0:14:11
0:14:11
 0:04:23
0:04:23
 0:07:57
0:07:57
 0:10:00
0:10:00
 0:04:25
0:04:25
 0:03:16
0:03:16
 0:23:11
0:23:11
 0:08:07
0:08:07
 0:06:17
0:06:17