filmov
tv
Solving the Exponential Equation e^x=ex
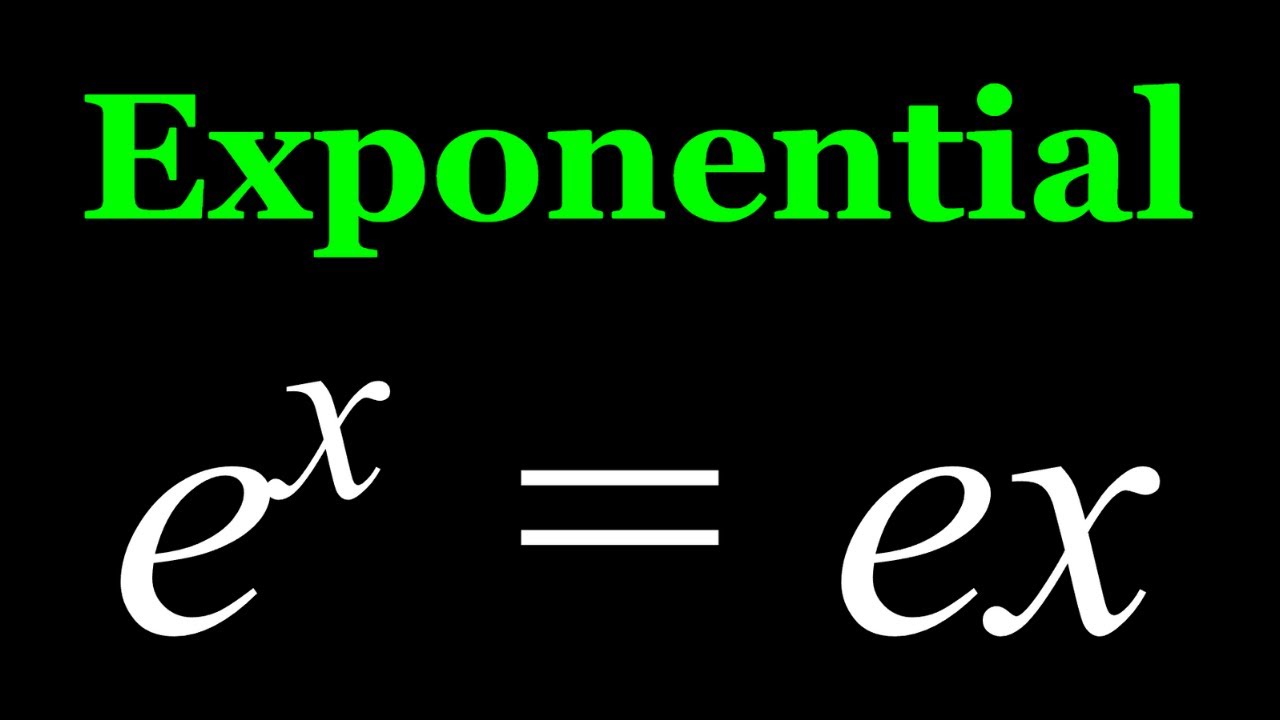
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #ExponentialEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
Solving the Exponential Equation e^x=ex
Solving Exponential Equations
Exponential Equations - Algebra and Precalculus
How do you solve an exponential equation with e as the base
Solve the Exponential Equation e^(2x-1)+2=3
Solve (e^x+e^(-x))/2 = 3
Solve the equation: e^x-1=0
Solving the Exponential Equation e^(3x - 1) = (e^x)^2
Solving Exponential equations
Classwiz How-To: Solving an Exponential Equation
The Exponential Function e and The Natural Log ln
Ex: Solve an Exponential Equation Using Logarithms
SOLVING EXPONENTIAL EQUATIONS: Base e
Ex: Solve a Exponential Equation with Base e Using Logarithm Definition (Multiple Steps)
A Nice Exponential Equation (e^x=x^e)
Can you solve this? | Exponential Equation | Algebra Problem.
Solve the Exponential Equation e^2x = e^x + 6 using a u-sub
Ex 4: Solve Exponential Equations Using Logarithms
Solve: e^(2x) - e^x - 6 = 0
Solving an Equation with The Exponential Function: e^(2x + 3) - 7 = 0
Ex: Solve a Basic Exponential Equation with Base e Using Logarithm Defintion
Ex 5: Solve Exponential Equations with Two Exponential Parts Using Logarithms
Can You Solve this Exponential Equation Involving Pi? Think out-side-the-Box| Step-by-Step Tutorial
Converting an exponential equation to logarithmic
Комментарии
 0:05:52
0:05:52
 0:16:36
0:16:36
 0:05:58
0:05:58
 0:02:47
0:02:47
 0:01:15
0:01:15
 0:03:22
0:03:22
 0:02:39
0:02:39
 0:00:55
0:00:55
 0:02:49
0:02:49
 0:01:14
0:01:14
 0:10:16
0:10:16
 0:04:01
0:04:01
 0:06:24
0:06:24
 0:04:22
0:04:22
 0:09:59
0:09:59
 0:03:33
0:03:33
 0:02:23
0:02:23
 0:05:18
0:05:18
 0:04:44
0:04:44
 0:02:04
0:02:04
 0:04:22
0:04:22
 0:05:41
0:05:41
 0:03:20
0:03:20
 0:02:31
0:02:31