filmov
tv
Permutation Problem: Sitting in a Circle/Table

Показать описание
Arrangements in a circles: This video will take you through finding the total possible arrangement of n people in a circle or at a table.
Permutation Problem: Sitting in a Circle/Table
Permutation : boys and girls sit alternate
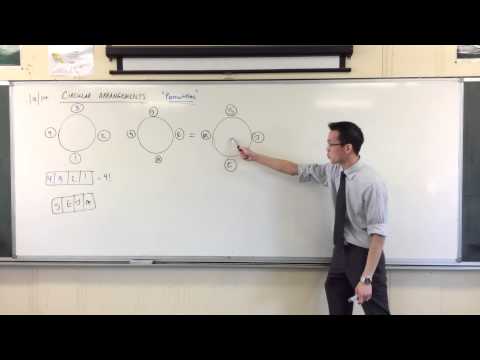
Introduction to Circular Arrangements
10 Boys & Girls Round a Table (1 of 2: Simple Conditions)
Not Sitting Together In a Row | Permutation
Permutations with restrictions - items not together | ExamSolutions
FSC-1 Mathematics CIRCULAR PERMUTATION- Problem Solving (A-level)
Number of ways 4 couples sit in a row with couples together IIT JEE
Permutation - Two couple at the round table question
Permutation and Combination - Girls and Boys in a Row problem
Solving Problems Part 3-Word and people arrangement problems(Permutations and combinations)
🪑Permutation Help: HOW MANY WAYS CAN 3 GIRLS SIT TOGETHER IN A ROW OF 7 CHAIRS? 👧
Combination and Permutation Problems with Answers (Grade 10 Math Lesson)
No Two Brothers Sit Together | Permutation & Combination | CAT/MAT/Management Exams
Solving Complex Problems that involves Permutation - Math Tutorials
Superpermutations: the maths problem solved by 4chan
CIRCULAR PERMUTATION: ROUND TABLE PROBLEM
How to Do Combinations: A GRE and GMAT Introduction by Top-Score Tutor
Factorial and counting seat arrangements | Probability and Statistics | Khan Academy
Permutation formula | Probability and combinatorics | Probability and Statistics | Khan Academy
Permutations and Combinations : Circular Permutation (11th/ JEE / GMAT/ CAT/ GRE/ Placement)
Permutation Part 3 | Circular Permutation | Algebra #maths #math #mathproblem
Circular Permutation | Round Table Problems
Permutation Arrangement problems
Комментарии
 0:05:08
0:05:08
 0:04:21
0:04:21
 0:06:10
0:06:10
 0:05:59
0:05:59
 0:02:47
0:02:47
 0:08:10
0:08:10
 0:05:21
0:05:21
 0:09:38
0:09:38
 0:05:44
0:05:44
 0:06:21
0:06:21
 0:07:15
0:07:15
 0:06:22
0:06:22
 0:04:45
0:04:45
 0:11:22
0:11:22
 0:09:02
0:09:02
 0:20:31
0:20:31
 0:04:38
0:04:38
 0:10:04
0:10:04
 0:09:00
0:09:00
 0:07:34
0:07:34
 0:10:23
0:10:23
 0:00:59
0:00:59
 0:15:17
0:15:17
 0:06:52
0:06:52