filmov
tv
Linear Algebra - Lecture 31 - Coordinate Systems

Показать описание
In this video, I review the definition of basis, and discuss the notion of coordinates of a vector relative to that basis.
The properties of a basis of a subspace guarantee that a vector in that subspace can be written as a linear combination of the basis vectors in only one way. The weights in that unique linear combination are called the coordinates of the vector relative to that basis.
The properties of a basis of a subspace guarantee that a vector in that subspace can be written as a linear combination of the basis vectors in only one way. The weights in that unique linear combination are called the coordinates of the vector relative to that basis.
Linear Algebra - Lecture 31 - Coordinate Systems
Linear Algebra - Lecture 31: The Dimension of a Subspace
Linear Algebra - Lecture 31 - Linearly Independent Sets and Bases
Linear Algebra: Lecture 31: complex vector spaces and complexification
Linear Algebra - Lecture 31/32 (modified) - The Basis of a Null Space
Lecture 31: Linear Algebra ( Some basic results on Linearly dependent vectors )
31. Eigenvectors of Circulant Matrices: Fourier Matrix
Gil Strang's Final 18.06 Linear Algebra Lecture
Linear Algebra 31 | Inverses of Linear Maps are Linear
Properties of determinants of matrices | Lecture 31 | Matrix Algebra for Engineers
Linear Algebra 31 | Inverses of Linear Maps are Linear [dark version]
Algebra - Ch. 34: Solving Systems of Linear Equations (1 of 31) What is a System of Linear Equations
Linear Algebra 14TBD: The Transpose Property of the Determinant
Algebra - Ch. 34: Solving System of Linear Equations (12 of 31) Inverse Matrix: Method 7: Part 1
a linear algebra problem
Advanced Linear Algebra - Lecture 31: Sylvester's Criterion for Positive Definiteness
Circles and spheres via dot products I | Wild Linear Algebra A 31 | NJ Wildberger
Eigenvalue Power Method (Example) | Lecture 31 | Numerical Methods for Engineers
Algebra - Ch. 31: Linear Inequality in 2 Variables (1 of 14) What is a Linear Inequality in 2 Variab
Theorem: Every Finite Dimensional Vector Space Contains a Basis | Linear algebra | (Lecture 31)
Linear Algebra: Ch 3 - Eigenvalues and Eigenvectors (31 of 35) Power Method A^n, General Eqn.***
Algebra - Ch. 34: Solving System of Linear Equations (11 of 31) Reduced Row Echelon Form: Method 6
Linear Algebra 31, Minkowsky Inequality, Triangular Inequality Proof
Algebra - Ch. 34: Solving System of Linear Equations (9 of 31) Row Echelon Form: Method 5: Part 1
Комментарии
 0:12:53
0:12:53
 0:16:45
0:16:45
 0:15:54
0:15:54
 0:52:26
0:52:26
 0:09:56
0:09:56
 0:22:11
0:22:11
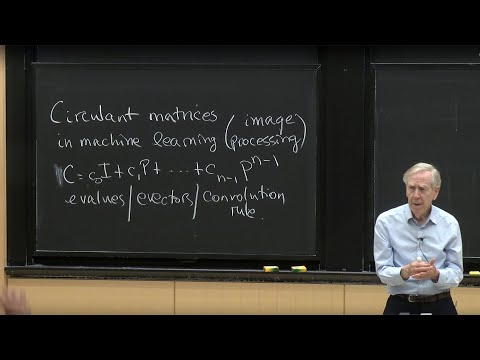 0:52:37
0:52:37
 1:05:09
1:05:09
 0:07:04
0:07:04
 0:15:21
0:15:21
 0:07:04
0:07:04
 0:03:26
0:03:26
 0:12:30
0:12:30
 0:05:54
0:05:54
 0:00:41
0:00:41
 0:09:49
0:09:49
 0:41:58
0:41:58
 0:07:48
0:07:48
 0:02:51
0:02:51
 0:11:49
0:11:49
 0:05:07
0:05:07
 0:05:54
0:05:54
 0:04:35
0:04:35
 0:04:52
0:04:52