filmov
tv
Calculus 2, Lec 26A, Absolute Convergence, Geometric Series, Power Series, Interval of Convergence
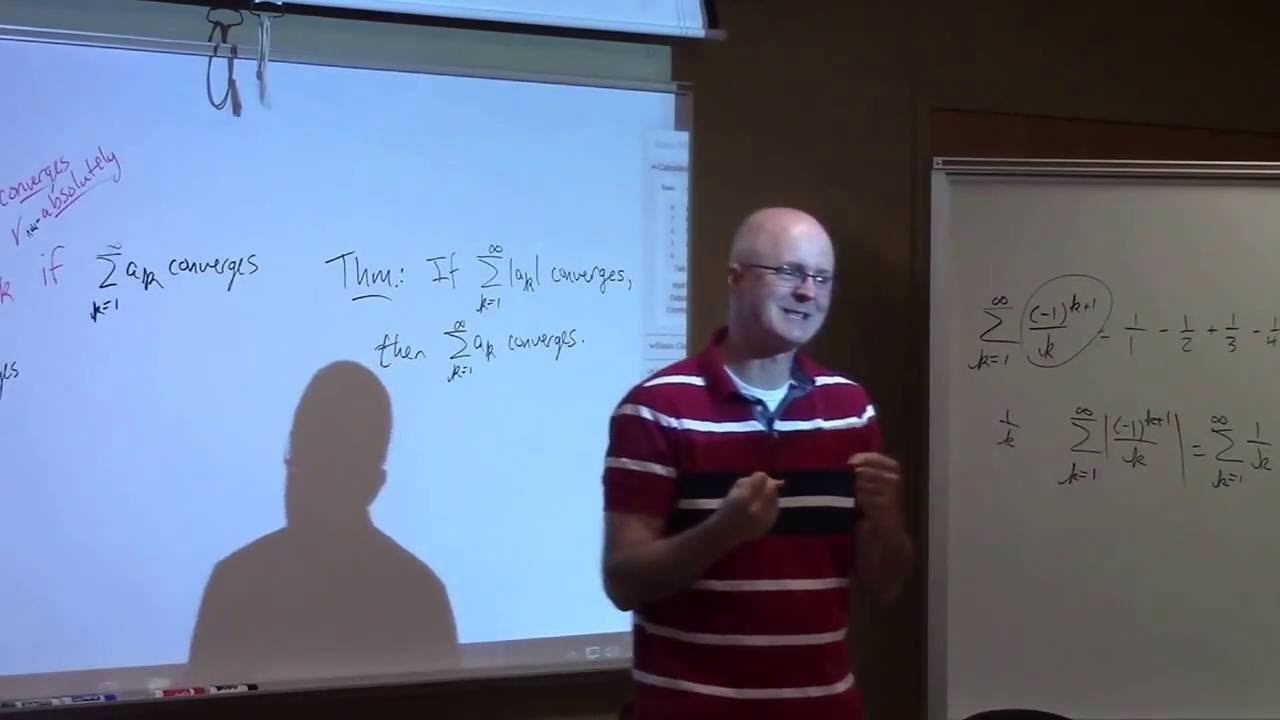
Показать описание
Calculus 2, Lecture 26A: Absolute Convergence, Geometric Series, Power Series, Interval of Convergence.
(0:00) Plan for the lectures and reminder about career night. (1:24) Absolute convergence versus non-absolute (conditional) convergence. (4:02) Example 1: a convergent alternating series that is also absolutely convergent (alternating p-series with p = 2). (7:00) Non-absolute convergence (often called "conditional convergence"). (8:30) Example 2: the alternating harmonic series is non-absolutely convergent (it converges by the alternating series test, but the corresponding series of positive terms is the harmonic series, which diverges). (9:32) Absolutely convergent series are more "robust" (the order of the terms can be switched around without changing the sum) while this is not true for non-absolutely convergent series (they are "fragile"). (12:09) Example 3: A geometric series that is also a power series. Find what it converges to and the interval of convergence. Also find the radius of convergence with the Ratio Test. (23:25) Example 3 (continued): the given geometric series can considered to be a function of x that can be graphed and compared. (28:12) Animation of graphs of the limiting function and the partial sum functions.
(0:00) Plan for the lectures and reminder about career night. (1:24) Absolute convergence versus non-absolute (conditional) convergence. (4:02) Example 1: a convergent alternating series that is also absolutely convergent (alternating p-series with p = 2). (7:00) Non-absolute convergence (often called "conditional convergence"). (8:30) Example 2: the alternating harmonic series is non-absolutely convergent (it converges by the alternating series test, but the corresponding series of positive terms is the harmonic series, which diverges). (9:32) Absolutely convergent series are more "robust" (the order of the terms can be switched around without changing the sum) while this is not true for non-absolutely convergent series (they are "fragile"). (12:09) Example 3: A geometric series that is also a power series. Find what it converges to and the interval of convergence. Also find the radius of convergence with the Ratio Test. (23:25) Example 3 (continued): the given geometric series can considered to be a function of x that can be graphed and compared. (28:12) Animation of graphs of the limiting function and the partial sum functions.
 0:34:42
0:34:42
 0:22:14
0:22:14
 0:32:05
0:32:05
 0:33:28
0:33:28
 0:21:36
0:21:36
 0:27:53
0:27:53
 0:57:09
0:57:09
 0:25:13
0:25:13
 0:31:51
0:31:51
 0:09:42
0:09:42
 0:11:44
0:11:44
 0:09:24
0:09:24
 1:17:27
1:17:27
 0:37:00
0:37:00
 0:43:07
0:43:07
 0:49:08
0:49:08
 0:03:10
0:03:10
 0:43:20
0:43:20
 0:11:08
0:11:08
 0:58:26
0:58:26
 1:17:35
1:17:35
 0:44:47
0:44:47
 0:59:46
0:59:46
 0:49:56
0:49:56