filmov
tv
Calculus 1, Lec 26B: Graphs & Slope Field of Logistic Model Solutions, Related Rates Introduction
Показать описание
See solutions follow the slope field for differential equations dy/dt=f(t,y). Introduce related rates problems as well.
(0:00) Review the meaning of the Mathematica Manipulate animation from Lecture 26A about maximizing the viewing angle.
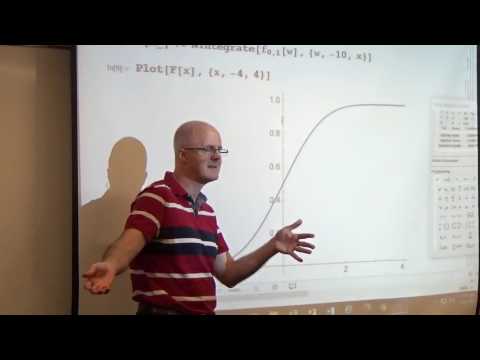
(1:34) Logistic differential equation model of population growth. Show formula and graph in Mathematica.
(6:10) Make a slope field to understand why the solution looks the way it does. Describe the idea of how to make a slope field and why solution curves must follow it. The little line segments must be tangent to solution curves that pass through their midpoints.
(10:17) Simpler Example: dy/dx = y with solutions y = C*e^(x). Show the slope field.
(15:27) Related Rates Example 1: the height of a right triangle is decreasing at a certain rate with respect to time, what is the rate of change of its area with respect to time?
(20:57) Related Rates Example 2: gasoline is pouring into a cylindrical tank and the height is increasing at a certain rate with respect to time, what is the rate of change of the volume with respect to time?
(24:43) Related Rates Example 3: A spherical snowball is melting and its radius is decreasing at a certain rate with respect to time, find the rate of change of the volume with respect to time.
(0:00) Review the meaning of the Mathematica Manipulate animation from Lecture 26A about maximizing the viewing angle.
(1:34) Logistic differential equation model of population growth. Show formula and graph in Mathematica.
(6:10) Make a slope field to understand why the solution looks the way it does. Describe the idea of how to make a slope field and why solution curves must follow it. The little line segments must be tangent to solution curves that pass through their midpoints.
(10:17) Simpler Example: dy/dx = y with solutions y = C*e^(x). Show the slope field.
(15:27) Related Rates Example 1: the height of a right triangle is decreasing at a certain rate with respect to time, what is the rate of change of its area with respect to time?
(20:57) Related Rates Example 2: gasoline is pouring into a cylindrical tank and the height is increasing at a certain rate with respect to time, what is the rate of change of the volume with respect to time?
(24:43) Related Rates Example 3: A spherical snowball is melting and its radius is decreasing at a certain rate with respect to time, find the rate of change of the volume with respect to time.
0:27:53
0:05:59
0:31:19
0:13:45
0:23:37
0:31:03
0:33:28
0:30:47
0:20:25
0:13:34
0:37:30
0:34:42
0:14:12
0:28:08
0:35:34
0:33:54
0:59:51
0:32:05
0:10:39
0:08:52
0:25:13
0:33:02
0:31:28
0:26:36